Combination
Circuits (430 only)
Combination circuits combine the features of parallel circuits with those of series circuits. The key to surviving these is to keep in mind the distinctive features of those circuits in mind.
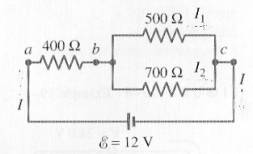 Example
1
Example
1
- What is the overall resistance of this circuit?
(1) First we tackle the parallel
part. The 500 and 700 W resistors are in parallel. Their equivalent resistance is Rp
= [500-1 + 700-1]-1 = 292 W.
(2) But this parallel branch is in
series with the 400 W
resistor. So the total resistance is RT=
400 + 292 = 692 W.
- What is the potential difference measured from a to b?
A common
mistake is to assume itís 12 V. But the 400 W resistor is in series with
the parallel branch of the circuit, and voltage is not constant in series.
But V400 W
= I R , so we just need to find the overall
current.
VT
= IT (RT)
12 = IT
(692)
IT =
0.0173 A or 17.3 mA.
V400
W = I R = 0.0173(400) = 6.94
V.
- What currents would be measured within the parallel branch? (see diagram for I1 and I2)
Voltage
is constant in a parallel branch. To find this voltage, use the result in (b).
Vparallel
= VT - V400 W
= 12 - 6.94 = 5.06 V.
Now apply
Ohmís Law:
I1 = V/R1 = 5.06/500 = 0.0101 A or 10.1 mA
I2
= V/R2 = 5.06/700 = 0.00723 A or 7.2 mA
(Note how
I1 + I2 = IT. This is a good way of verifying
your answers.)
Example 2
a.†† Find the total current in the following:
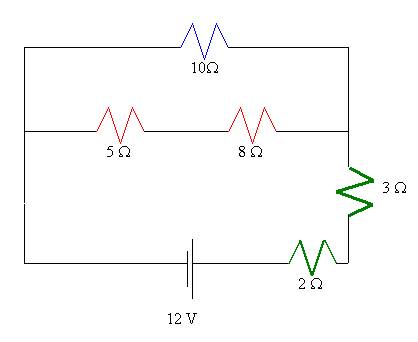
First,
weíll redraw the circuit to make sure we realized that the 5 and 8 W resistor
are in series, but they in turn are in parallel to the 10 W
resistor. The parallel branch is then series with both the 3 and 2 W
resistors.
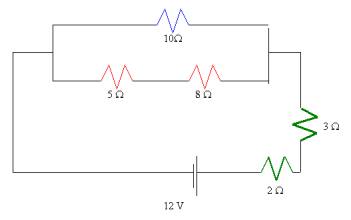
In short
RT = 2 + 3 + RP
RPARALLEL = [10-1 + (5 + 8)-1]-1 = 5.65
W
RT
= 2 + 3 + 5.65 W =10.65 W
VT =
ITRT
IT =
VT / RT = 12/10.65 = 1.1 A
- What is the voltage drop across the 8 W resistor?
VPARALLEL = IT RPARALLEL = 1.1(5.65) = 6.22 V; voltage is constant in parallel, but the problem is that the 8 W resistor is in series with the 5 W resistor. So we have to divide this voltage by the combined series resistance in that branch to get its current:
6.22/(5 + 8) = 0.478 A
V8W = I R = 0.478(8) = 3.83 V
†