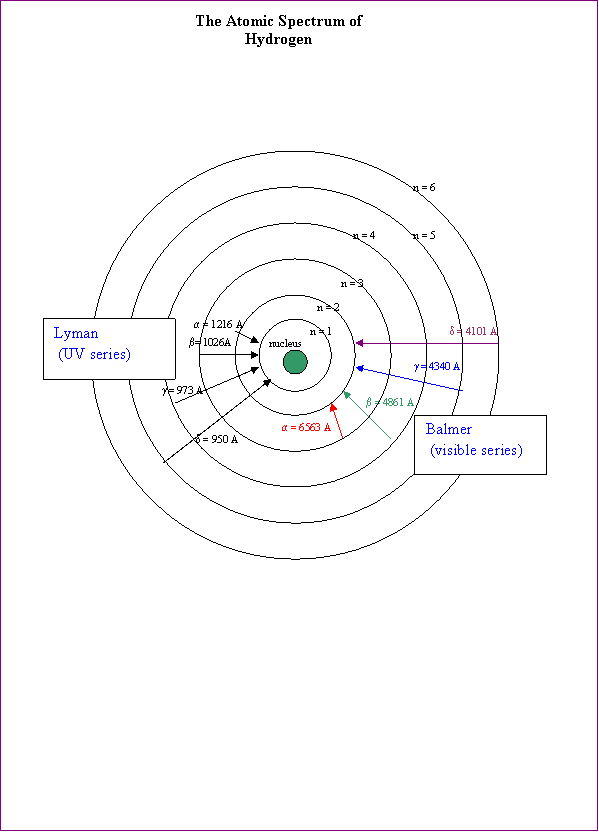
 Hydrogen’s sole electron can absorb varying
amounts of energy. Imagine quadrillions of exited atoms. (How
does one imagine quadrillions!?) In some atoms, for example, the excited
electron may have only reached the n = 3 level. Upon returning to the n = 2
level, these atoms will emit light with a wavelength corresponding to the red
colour. In the so-called Balmer series, most of the
emissions are visible. These include the n = 6 to 2(violet), n = 5 to 2(blue),
n = 4 to 2(blue-green), and as mentioned, the n = 3 to 2(red).
Hydrogen’s sole electron can absorb varying
amounts of energy. Imagine quadrillions of exited atoms. (How
does one imagine quadrillions!?) In some atoms, for example, the excited
electron may have only reached the n = 3 level. Upon returning to the n = 2
level, these atoms will emit light with a wavelength corresponding to the red
colour. In the so-called Balmer series, most of the
emissions are visible. These include the n = 6 to 2(violet), n = 5 to 2(blue),
n = 4 to 2(blue-green), and as mentioned, the n = 3 to 2(red).
But can’t the electron return to its ground state?
Yes, but the emissions form such transitions fall in the invisible ultraviolet
spectrum. These are the so-called Lyman series.
For any series, the wavelength of
the radiation emitted can be calculated by using two formulas:
(1)First to calculate the energy emitted, DE, from the electron:
DE = -R( 1/nf2 – 1/ni2)
where R = rydberg’s
constant = 2.178 X 10-18 J
nf = final energy level
ni = initial energy level
(2) to obtain the wavelength
associated with the energy:
l = hc/ -DE
where h = Planck’s constant = 6.626 X 10-34 Js
c = speed of light = 2.9979 X 108
m/s
To convert to angstroms, A, multiply by A/10-10m
|
Balmer |
|
E(J) |
l (A) |
|
nf |
ni |
|
|
|
2 |
6 |
-4.8400E-19 |
4.103E+03 |
|
2 |
5 |
-4.5738E-19 |
4.343E+03 |
|
2 |
4 |
-4.0838E-19 |
4.864E+03 |
|
2 |
3 |
-3.0250E-19 |
6.567E+03 |
|
Lyman |
|
|
|
|
nf |
ni |
|
|
|
1 |
5 |
-2.0909E-18 |
9.500E+02 |
|
1 |
4 |
-2.0419E-18 |
9.728E+02 |
|
1 |
3 |
-1.9360E-18 |
1.026E+03 |
|
1 |
2 |
-1.6335E-18 |
1.216E+03 |