Momentum,
Kinetic Energy and the Discovery of the Neutron

before elastic collision
Consider two masses, m1
and m2, about to collide head on. If their collision is
perfectly elastic, the total momentum and kinetic energy of the system will be
conserved. (in an inelastic collision--the masses lock
together--- only momentum is conserved)
after elastic collision
Since kinetic energy is
conserved:
0.5 m1v12
+ 0.5 m2v22 = 0.5 m1v1'
2 + 0.5 m2v2' 2
or
0.5 m1v12
- 0.5 m1v1' 2 = 0.5 m2v2'
2 - 0.5 m2v22
First we will divide
through by 0.5, then take out a common factor of m1
and then we will factor the difference of squares:
m1(v1 - v1')(v1
+ v1') = m2(v2 - v2')(v2
+ v2') or
(m1v1 - m1v1')(v1 + v1')
= ( m2v2
- m2v2') (v2 + v2')
But the terms in bold
are the changes in momentum experienced by each ball. Since whatever momentum
is gained by one ball is gained by the other, these terms cancel and we are
left with v1 + v1' = v2 + v2'.
(1)
Momentum:
m1v1
+ m2v2 = m1v1'
+ m2v2'
(2)
But since, from rearranging
equation(1), v2' = v1 + v1'
- v2 , it can be substituted this into equation(2):
m1v1
+ m2v2 = m1v1'
+ m2(v1 + v1' - v2 )
Solving for v1'
we obtain
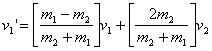 (3)
(3)
Similarly if we isolate v2'
in equation (1) and substitute it into eqn (2) and
then solve for v2' we obtain:
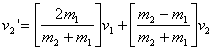 (4)
(4)
What is all this have to do with the discovery of the neutron? When alpha
particles (equivalent to a helium nucleus) from
the radioactive element polonium bombarded beryllium, Be, invisible particles
of mass m1 were emitted. These struck either N nuclei or protons
initially at rest, and Chadwick then measured the resulting velocities of the
moving nuclei, v2'
Since the nuclei were
initially at rest, v2 = 0. So equations (3) and (4) simplify to:
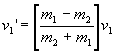 (5) and
(5) and 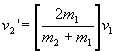 (6)
(6)
Chadwick compared the speed
v2' for nitrogen to that of hydrogen when each collided with the
mysterious component(neutron) emitted from berylliumís
nucleus: Note that N is 14 times more massive than H(corresponding to subscript
2), and the subscript 1 refers to the neutron.
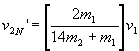 and
and 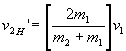
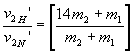
This ratio, according to
his experiments, turned out to be 7.5. From this he concluded that m1,
the mass of the unknown particle emitted by beryllium, was about the same as
that of the proton, m2. Chadwick had found an essential property of
the previously unknown neutron by applying the conservation of momentum and
kinetic energy principles to subatomic particles. Note that in the case of a
collision with a stationary proton, the neutron should end up with a velocity
of zero (see equation(5) ). This is similar to hitting
a cue ball head on with another ball. The cue ball will stay put after the collision.
Here is Chadwick's original
paper.
References
Serway, Richard A. Physics for
Scientists and Engineers. Saunders. 1983.
Haber-Schaim, Uri and al. PSSC Physics 3rd Edition. Heath. 1971.
Martindale, David G. and al. Physics: A Senior Course. Heath
Giancoli, Douglas C. Physics. Prentice Hall. 1995.