Equil'm Law Expression Problems( continued)
9. A 1.00 L vessel has initially 7.00 g of CO(g) and 4.50 g of steam. If K = 3.59, how many grams of CO2 were found at equilibrium?
CO(g) + H2O(g)
= H2(g) + CO2(g)
|
|
CO(g) |
H2O(g) |
H2(g) |
CO2(g) |
|
Initial number of Moles /L |
7/(12+16 g/mole)/1.0 L= 0.25moles/L |
4.5/(2+16 g/mole)/1.0 L= 0.25 |
0 |
0 |
|
Moles /L reacting/forming |
x |
x |
x |
x |
|
Moles /L at equil'm |
0.25 - x |
0.25- x |
x |
x |
x2/(0.25-x) (0.25-x) = 3.59
0 = 0.2243750000 -1.795000000x + 2.59x2
x = 0.1636361455, or 0.5294140475
But x cannot be greater than original number of
moles, so x = 0.1636361455 = 0.16 moles/L.
in one liter:
0.16 moles (44g/mole) = 7.0 g.
10. Very sneaky problem!
[HI]2/([H2][I2])
= Ka
[HI]2/[0.0007/1][0.00413/1] = 55.6
[HI] = 0.0127 moles/L (don't round off too much!)
V = 1.00 L but it contains three gases! So
for n you have to add all the moles
n = 0.0127 + 0.0007 +
0.00413 = 0.01753moles
T = PV/(nR) = 101(1)/(0.01753*8.31) =
693 K
11. At equilibrium there are only 1.7 X 10-2 moles of Pb+2 present for every liter of solution. What K is the K for the following reaction?
PbCl2(s) = Pb+2(aq) + 2 Cl-(aq)
K = [Pb+2][ Cl-(aq)]2
= [1.7 X 10-2][2 X 1.7 X 10-2]2
=0.000020
12. Given: CO(g) + H2O(g)
= H2(g) + CO2(g)
a. A student introduces 0.25 moles of CO and 0.25 moles of steam (H2O(g)) in a 1.00 L flask. If Keq at 800 C is 3.59 and temperature is constant, how much hydrogen will there be at equilibrium?
|
|
CO(g) |
H2O(g) |
H2(g) |
CO2(g) |
|
Initial number of moles/L |
0.25 |
0.25 |
0 |
0 |
|
moles/L reacting/forming |
x |
x |
x |
x |
|
moles/L at equil'm |
0.25- x |
0.25- x |
x |
x |
x2/(0.25-x) (0.25-x) = 3.59
0 = 0.2243750000 -1.795000000x + 2.59x2
x = 0.1636361455, or 0.5294140475
But x cannot be greater than original number of
moles, so x = 0.1636361455 = 0.16 moles/L.
Concentration [H2] = 0.16 moles/L
b. Repeat for K = 6.00.
|
|
CO(g) |
H2O(g) |
H2(g) |
CO2(g) |
|
Initial number of moles/L |
0.25 |
0.25 |
0 |
0 |
|
moles/L reacting/forming |
x |
x |
x |
x |
|
moles/L at equil'm |
0.25- x |
0.25- x |
x |
x |
x2/(0.25-x)2= 6
0 = 0.375 - 3x + 5x2
x = 0.1775255129, 0.4224744871 But x cannot be greater than original number of moles, so x = 0.1775255129= 0.18 moles/L
Concentration [H2] = 0.18 M.
13. Given : N2(g) + 3H2(g)
= 2 NH3(g)
At 400 C, [N2(g)]eq= 0.45 M
[H2(g)]eq= 1.10 M
If K = 1.7 X 10-2, find the equilibrium concentration of NH3.
N2(g) + 3H2(g) = 2 NH3(g)
|
|
N2(g) |
H2(g) |
NH3(g) |
|
Initial number of moles |
Doesn't matter here. |
Doesn't matter |
Doesn't matter |
|
Moles reacting/forming |
Doesn't matter |
Doesn't matter |
Doesn't matter |
|
Moles at equil'm |
0.45 |
1.10 |
x |
x2/[(0.45)(1.10)3]= 1.7 X 10-2 ( note volume = 1 L; they gave us actual concentrations in
moles/L)
x = 0.100 M
Concentration [NH3(g)]
= 0.100 M.
14. Given : H2(g) + I2(g)
= 2 HI(g)
[H2(g)]eq= 0.200 M
[I2(g)]eq= 0.200 M
If K = 55.6, find the equilibrium concentration of [HI]eq
H2(g) + I2(g) = 2 HI(g)
|
|
H2(g) |
I2(g) |
HI(g) |
|
Initial number of moles |
Doesn't matter here. |
Doesn't matter |
Doesn't matter |
|
Moles reacting/forming |
Doesn't matter |
Doesn't matter |
Doesn't matter |
|
Moles at equil'm |
0.200 |
0.200 |
x |
x2/[(0.200)(0.200)]= 55.6 (
note volume = 1 L; they gave us actual concentrations in moles/L)
x = 1.49
Concentration [HI] = 1.49 M.
15. Given : W(g) + X(g) = U(g) + V(g) + T(g)
a. A student introduces W and X into a flask. The initial concentration of each reactant is 0.80 mole/L. Slowly they reach equil'm and [U]eq = 0.60 mole/L. Find K.
W(g) + X(g) = U(g) +
V(g) + T(g)
|
|
W(g) |
X(g) |
U(g) |
V(g) |
T(g) |
|
Initial number of moles |
0.80 |
0.80 |
0 |
0 |
0 |
|
Moles reacting/forming |
W/U=1:1, so W= 0.60 |
X/U=1:1, so W= 0.60 |
0.60 |
V/U = 1:1,so V= 0.60 |
T/U = 1:1,so T= 0.60 |
|
Moles at equil'm |
0.80-0.60 =0.20 |
0.80-0.60 =0.20 |
0.60 |
0.60 |
0.60 |
(0.60) (0.60) (0.60) /[(0.20)(0.20)]=
K( note volume = 1 L; they gave us actual concentrations in moles/L)
K = 5.4.
b. The experiment is repeated at a different temperature in a 2.0 L flask. If K = 0.5, and if there were initially 0.40 moles of W2 and 0.40 moles of X2, what expression could be used to solve for the number of moles of U found at equil'm? ( Don't attempt to solve the expression.)
W(g) + X(g) = U(g) + V(g) +
T(g)
|
|
W(g) |
X(g) |
U(g) |
V(g) |
T(g) |
|
Initial number of moles |
0.40 |
0.40 |
0 |
0 |
0 |
|
Moles reacting/forming |
x |
x |
x |
x |
x |
|
Moles at equil'm |
0.40 - x |
0.40 - x |
x |
x |
x |
(x/2) (x/2) (x/2) /[(0.40 - x)/2( 0.40 - x)/2]= 0.5( note volume = 2 L)
16. At 2000 C, K for the following reaction = 1.6 X 10-3.
2 NO(g) = N2(g) +
O2(g)
If there was only NO introduced initially and we end up with an equilibrium concentration of 0.13 M for NO, what will be the concentration of both nitrogen and oxygen at equilibrium?
2 NO(g) = N2(g) + O2(g)
|
|
NO(g) |
N2(g) |
O2(g) |
|
Initial moles/L |
Doesn't matter here. |
0 |
0 |
|
moles/L reacting/forming |
x |
x |
x |
|
moles/L at equil'm |
0.13 |
x |
x |
x2/(0.132)= 1.6 X 10-3.
x = 0.0052 moles
[N2(g)] = [O2(g)] = 0.0052 moles/L
17. a. When is Keq = 1 ?
For aB + cD = eF+ gH
Since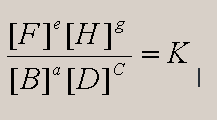 , if K=1, then [F]e[H]g
= [B]a[D]c.
, if K=1, then [F]e[H]g
= [B]a[D]c.
b. When is Keq
a large number?
If K= large number, then [F]e[H]g
>> [B]a[D]c.