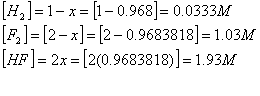Law of Chemical Equilibrium

 

Since a reaction at equilibrium has fixed concentrations of products and reactants, we can calculate a constant for a given reaction at constant temperature.

 

For the generalized equation

 

                                                aB + cD   eF + gH

 

                                                ,

 

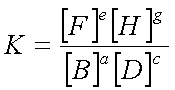where [ ] represents the equilibrium concentration in moles/L

 

 

 

Keep in mind: You only include concentrations of aqueous and gaseous reactants/ products, not those of liquids or solids. Liquid and solid concentrations remain constant and so they are imbedded in K.

 

Example 1        Write an equilibrium law expression for the following:

 

a.         H2(g) + F2(g)  2 HF(g)   

 

Answer                       

 

 

b.         ZnS(s)  Zn+2(aq) + S-2(aq)

 

Answer                               K = [Zn+2][S -2]

 

 

c.         H2O(l) H+(aq) + OH-(aq)

 

 

Answer                        K = [H+][OH -]

 

 

 

d.         6 XA(g) + Y2Z(l)  + A(g)2 X3Y(g)   +    A7(s)

 

 

Answer                       

 

Example 2

 

Given the following concentrations in moles/L at 748 C

 

  CO2(g)   +   H2(g)   CO(g)   +   H2O(g)  

0.00630           0.00630           0.00552               0.00552

 

Write the equilibrium law expression, and then calculate the constant at that temperature.

 

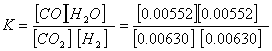= 0.768

 

 

Example 3

 

Suppose 6.000 mol of F2 and 3.000 mol of H2 are mixed in a 3.000 L container to make HF. The equilibrium constant at a certain temperature is 1.15x10 2.

Calculate the equilibrium concentrations, given:

 

H2(g) + F2(g)  2 HF(g)   

 

For another approach, which uses moles in the table rather than moles/L, click here.

 

In such problems, it is very important to distinguish between

(1)   the number of moles/L initially found in the reaction vessel

(2)   the number of moles/L that actually react or form

(3)   the number of moles/L found at equilibrium

 

 

 

 

1 H2(g)

1 F2(g)  

2 HF(g)   

Initial # of moles/L

3.000/3 = 1.000

6.000/3 = 2.000

0 (since it is not mentioned,we have to assume there was none introduced.

Moles/L reacting/forming

x, since we don’t know how much reacts

x, since the ratio of  H2(g) to F2(g)  in the equation is 1: 1

2x , since 2 moles of HF form for every 1 mole of  reacting H2.

# of moles/L at equilibrium

1-x remain

2-x remain

0 + 2x now exist.

 

We write an equilibrium law expression, and then substitute the equilibrium number of moles into that expression. Don’t forget to divide by the number of litres in the first row, which in this example is 3.0 L. Note that moles/L – moles/L = moles/L so that it would be incorrect to divide by 3.0 L again in the last row.

 

 

 

 

 

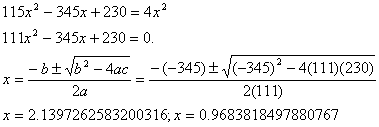
If we had only 1.00 mole/L of hydrogen initially,  is the only sensible answer.

Now we can wrap up the problem and calculate the equilibrium concentrations: