The Gas Laws
1. Charles'Law: applies to ideal gases under constant pressure.
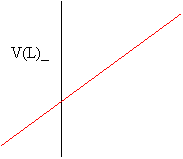
If you heat a gas, its volume, V, will expand at a rate that is directly proportional to its absolute temperature measured in Kelvin.
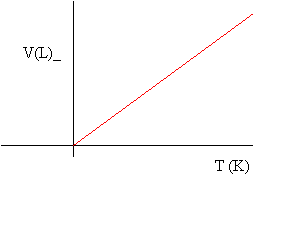
T (oC)
-273
Notice that a plot of volume versus temperature in degrees Celsius (oC) leads to an x-intercept of about -273. To obtain an x-intercept of 0, we add 273 to the Celsius temperature to obtain the absolute temperature measured in Kelvin. This leads to a simpler relationship known as Charles' Law:
at constant pressure
with T in Kelvin
Example: A 250 mL balloon is warmed under constant atmospheric pressure from 0.00 C to 20.0 C. Find its final volume.
(Assume that the rubber does not offer less resistance as it stretches: in reality it may and pressure would not be constant.)
Using Charles' Law:
V2 = 268 mL
2 Avogadro's Law: Under the same conditions of pressure and temperature, equal volumes of different gases have the same number of molecules, or in other words the same number of moles.
If the above are all at, say for example, room temperature and at atmospheric pressure, if the containers they are in are all of the same volume, then they all have the same number of moles. The size of the individual molecules is irrelevant. Conversely, if you were told that under certain conditions 10 moles of Ar occupied 224 L, then 10 moles of oxygen would also take up 224 L.
At OoC and under 101.3
kPa of pressure , one mole of any ideal gas occupies 22.4 L.
Example 1: At STP, how many litres of hydrogen gas would you collect by reacting 0.10 g of Na?
2 Na + 2 HCl --> 2 NaCl + H2(g)
First convert the Na to moles. 0.10g/23g/mole = 0.00435 moles of Na
Consider the ratio between Na and H2(g) in the equation and write a proportion.
2/0.00435 = 1/x
x = 0.00217 moles of H2(g)
Since conditions are STP, we can convert to L using 22.4 L/mole( the molar volume)
Answer =0.00217 moles of H2(g) (22.4L/mole) = 0.0487 L or 48.7 mL
Example 2: Find the density of Ar at STP and at -20 C and 101.3 kPa.
Consider 1 mole of Ar = 40 g/mole. At STP, the volume of 1 mole= 22.4 L, so its density becomes:
40 g /22.4 L = 1.8g/L
At -20 C, we need Charles Law to get its volume:
22.4/(0+273) = V2/-20+273
V2 = 20.8 L; so the density increases to 40g /20.8 L = 1.9 g/L
3. Boyle's Law: applies to ideal gases at constant temperature. The product of a gas' pressure and volume are constant, implying that
P1V1 = P2V2. at constant temperature.
The relation is an inverse one: if you double pressure, the volume becomes half of the original.
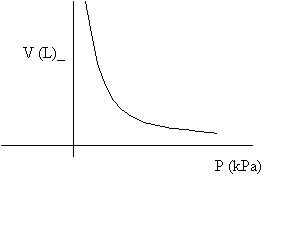
The curve is known as a hyperbola, and it reveals how volume decreases as more pressure is applied.
Example: At constant temperature, the pressure of a gas is increased threefold. The final volume of the gas is 36 L. what was the original volume?
P1V1 = P2V2. at constant temperature.
P2 = 3 P1.
Substitute: P1V1 = 3 P1(36 L)
Since P1 cancels, V1 = 3 (36) = 108 L.
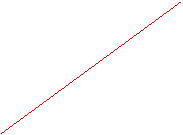
4. Gay-Lussac's Law: applies to ideal gases at constant volume. In a container of constant volume, the pressure is directly proportional to its absolute temperature (K).
P(kPa)_ T (K)
under constant
volume. Temp in K.
The graph reveals how increasing the temperature will cause the molecules to move faster, and since they are not permitted extra room for maneuvering, they collide more often, resulting in more pressure.
Example 1: At 300K, what pressure would be exerted by hydrogen gas if it exerts 200 kPa at 100 K?
200/100 = x/300
x = 600 kPa.