The Golden Ratio

 

1.                  Start with a square.

2. 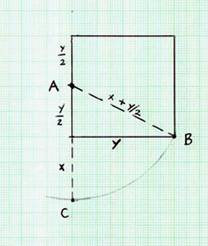                 Bisect one of its sides.

3.                  Draw a segment from A to B.

4.                  Use AB as a radius and extend to point C.

5.                  Use the Pythagorean theorem:

 

a2 + b2 = c2.

y2 + (y/2)2 = (x + y/2)2.

y2 = x2 +xy.

 

If we let x = 1 unit:

 

y2 = 12 +1y.

y2 – y – 1 = 0.

 

Solving by the quadratic formula:

 

 

The root that applies to the geometric situation is  .This is known as the golden ratio. Keeping in mind that y/x where x=1, then y/x = =1.6180339887498948482045868343656381177203091798057628…

 

(Strangely, this number reduced by one equals its inverse[y-1=1/y], and if increased by one, it equals its square.[y+1=y2])

 

If we go back to y2 = x2 +xy, and divide through by xy we obtain:

 

y
 
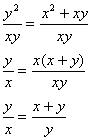                                                                   y                      x

 

This leads to the golden rectangle:

 

 

The Parthenon almost fits perfectly into the golden rectangle:

 

As first noted in Classical Greece, the ratio of the length of the human body to the height of the navel approximates the golden ratio (see vertical lines in in DaVinci’s drawing.). The ratio also appears in other aspects, as represented in the T formation, and in the ratio of the forearm’s length to that of the hand.

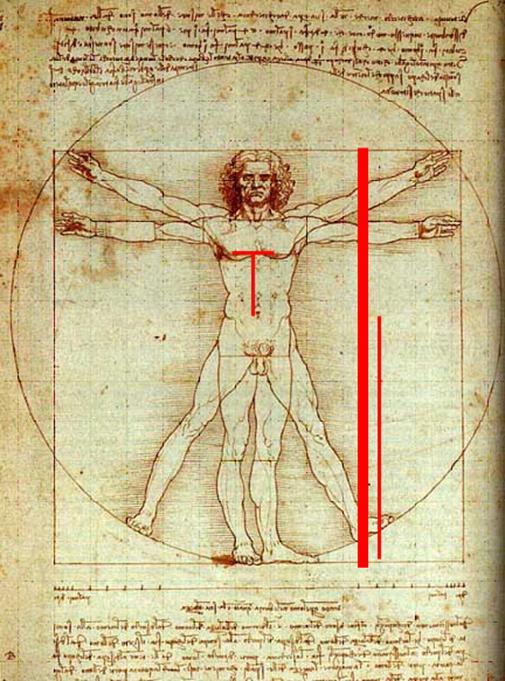
In the female form, the ratio of the circumference of either the torso or the hips to that of the waist is close to the golden ratio. For instance, 38 corresponds to 23.6 and 36 to 22.4, both of which are considered desirable attributes.

 

 

References:

 

Livio, Mario. The Golden Ratio. The story of Phi: Nature’s Most Remarkable Number. Broadway Books. 2003

 

Chernow and al., editors. Columbia Encyclopedia. 1993

 

http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibInArt.html