Solutions to p 17 (green book)
I've done some problems by proportion for those of you who prefer that method and I've also done some the faster way, like I often do it in class.
1. a. ![]()
NH3 O2
![]()
x = 2.50 moles of O2
![]()
b. 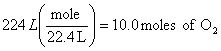
O2 NO
![]()
x = 8.00 moles of NO
![]()
![]()
c. NH3 O2
![]()
x = 2.5 moles O2

2. 47.3 ml = 0.0473 L of H2, so at STP (see conditions in problem)
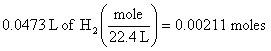
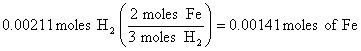
(this step is equivalent to a ratio used in previous solutions)
![]()
3. 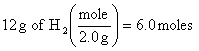
![]()
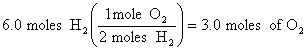
At 0oC and 101.3 kPa, we would have produced 3.0 X 22.4 L/mole = 67 L, but at
40oC and 101.3 kPa(we assume), we will produce more. According to Charles' Law,
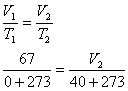
V2 = 77 L
4. 1.204 X 1024 molecules. Divide by Avogadro's number and you realize that we have 2.00 moles of Ne in container B.
Container A has 4 moles of Ar under the same conditions. With twice the number of moles, A must be twice as big in volume as B.
5. a. Consider 1.00 moles of Ar = 39.9 g and 22.4 L at STP, so its STP density is 39.9 g/22.4 L = 1.78 g/L
b. At -50oC, using Charles' Law the volume of 1.00 moles of Ar is reduced to 18.3 L, so its
density increases to 39.9 g/18.3 L = 2.18 g/L
6. from the board:
Question was:
Given, 3 H2 + N2 à2 NH3
If 11.2 L of H2 and 11.2
L of N2 are mixed, what’s the most NH3 that can be
produced? Which gas will be in excess, and how many liters will be in excess?
Solution:
Longer Method
11.2 L of an ideal gas is 0.500 moles at STP
So we have 0.500 moles of hydrogen and 0.500 moles of nitrogen.
3 H2 + N2 à2 NH3
If you assume that 0.500 moles of N2 react, then according to the ratio , you would need 3*0.500 =1.500 moles of hydrogen. But we only have 0.500, so the N2 can’t all be reacting.
If we assume that all 0.500 moles of H2 react, then only 0.500/3 moles of N2 react, which means that there will be 0.500 – 0.500/3 leftover moles of N2 = 0.333..moles = 7.47 L leftover nitrogen.
Since all 0.500 moles of H2 react, according to
the ratio, 2/3(0.500) moles of NH3 are produced = 0.333..moles =
7.47 L of NH3.
Shorter Method(L of ideal gases are proportional to moles
at same T,P (avogadro’s Hypothesis))
We have 11.2 L of hydrogen and 11.2 L of nitrogen.
3 H2 + N2 à2 NH3
If you assume that 11.2 L of nitrogen of N2 react, then according to the ratio , you would need 3*11.2 L =33.6 L of hydrogen. But we only have 11.2 L, so the N2 can’t all be reacting.
If we assume that all 11.2 L of H2 react, then only 11.2 L/3 moles of N2 react, which means that there will be 11.2 – 11.2/3= 7.47 L leftover nitrogen.
Since all 11.2 L of H2 react, according to the
ratio, 2/3(11.2 L) = 7.47 L of NH3.