The Ideal Gas Law
Recall that at constant volume, the relationship between pressure and temperature(K) is a direct variation:
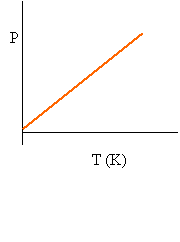
Since the relationship is linear, we can say that P/T = m1.
The relationship between volume, V, and the number of moles, n, is also linear, assuming constant pressure and volume. (Avogadro's Hypothesis). If you double the number of particles or moles of particles, you will double the volume.

n
Since the relationship is linear, we can say that V/n = m2.
Multiply the above fractions: ![]() Let m1m2 = a new
constant, R, and cross multiply:
Let m1m2 = a new
constant, R, and cross multiply:
PV = nRT.
To get the value of R, we can substitute familiar STP conditions into the expression for R:
![]()
Note, however, that the gas constant R applies to all conditions. If we increase P, then volume will decrease accordingly and still produce 8.31.
Example 1 What is the volume occupied by 6.0 g of hydrogen(H2) at 30 oC if it was subjected to a pressure of 101.3 kPa?
6.0 g/(2.0 g/mole) = 3.0 moles of H2.
PV = nRT, so

Example 2 List three ways of increasing pressure.
Since
![]() , we
can
, we
can
(1) increase the amount of gas while keeping T and V constant.
(2) increase temperature while keeping n and V constant.
(3) decrease volume while keeping n and T constant.
Example 3 Calculate the molar mass of an unknown gas using the data
below:
Volume
of syringe: 0.100
L
Mass
of syringe + unknown gas 90.99
g
Mass of empty syringe 90.67 g
Temperature 30.0 C
Pressure 100 kPa
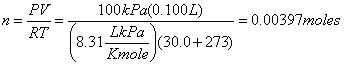
molar
mass = ![]()