Q22. Express 103(97) as a difference of squares.
A22. 103(97) = (100 + 3)(100 - 3)
= 1002 - 32 = 9991
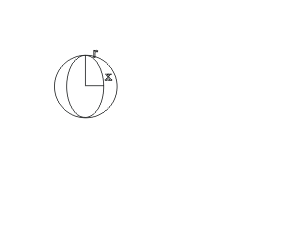
Q23. The shaded area between a circle of radius r and an ellipse is πr2/2. Find x.

A23. Shaded area = πr2/2 = πr2 - πab, where a = x and b =r.
πr2/2 = πr2 - πxr
r/2 = r - x
x = r/2.
Q24. What is the perimeter of the triangle defined by A( 0,0 ) , B( 4,0 ) and C( 4,4 ) ?
A24. Perimeter = AB + BC + CA
= 4 + 4 + 4√2 = 8 + 4√2
Q25. A cone-shaped cup and a cylinder have the same height and the same diameter. How many
cups of water from the cone are needed to fill the cylinder ?
A25. 3
Q26. The Pythagorean triple that includes 11 also includes two consecutive integers. Find them.
A26. 112 + x2 = (x+1)2
121 + x2 = x2 + 2x +1
x = 60
The full triple is 11, 60 and 61.
Q27. Find the distance between the plane and the horizon:
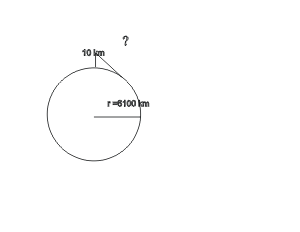
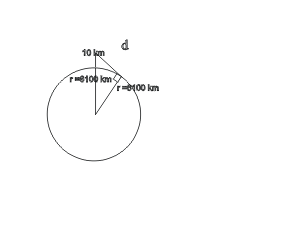
A27. d2 + 61002 = 61102.
d = 349 km.
Q28. The cost of two pizzas of the same thickness is proportional to area. A pizza 10 cm in diameter costs $5. How much should a 20 cm one cost ?
A28. (20/10)2($ 5) = $ 20.
Q29. Factor a3 + b3 + c3 -3abc
A29. (a + b + c)(a2 + b2 + c2- ab -ac -bc)
Q30. Why can't a Pythagorean triple include 3 odd numbers ?
A30. The square of any odd number is odd, and the sum of any two odd numbers is even. Since the square root of an even number is also even, then c = √(a2 +b2) would not be odd.
Q31. Find the next number in the sequence
2, 12, 36, 80, 150 , ...
A31. 2 = 12 + 13
12 = 22 + 23
36 = 32 + 33
sixth term = 62 + 63 = 252.
Q32. One way of testing whether 10277 is prime is to test its divisibility by all primes < y.
What should y be ?
A32. √10277 = 101.4. Incidentally 10277 = 43* 239.
Q33. How many real roots does the equation x4 + x3 + x2 + x = 0 have ?
A33. Just two. x4 + x3 + x2 + x = 0.
x3( x + 1) + x (x + 1) = 0.
(x + 1 )( x3 + x) = 0.
x(x+1)(x2+1) = 0.
so x = 0 or -1.
Q34. Express the area of the triangle in terms of angles A and B and its base d.
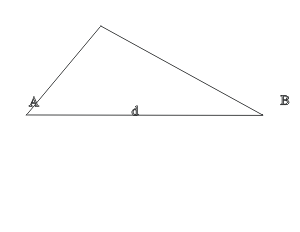
A34.
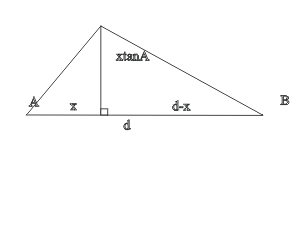
(continued)
xtanA = tanB (d - x)
xtanA = dtanB - xtanB
x(tanA + tanB) = dtanB
Q35. When reflected in y = x, the equation of a certain line remains unchanged. If this line passes through (2 , 2), what is its equation ?
A35. For the equation of a line to be unaffected after such a reflection, its slope must be -1.
y = mx + b
2 = -1(2) + b
b = 4
y = -x + 4
Q36. When expanded, ( 3x + 2 )6 has seven terms. What is the coefficient of the seventh term ?
A36. Using Pascal's triangle:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
The above line applies to a power of 6 so that:
(3x)6 + 6(3x)5(2) + 15(3x)4(22) + 20(3x)3(23) + 15(3x)2(24) + 6(3x)(25) + 26
The middle term's coefficient is 4320.
Q37. Why are sewer caps round and not square-shaped?
A37. The round cover sits on a lip that is smaller than the cover. Because its diameter is constant, the cover cannot fall through. Keep in mind that the diagonal of a square is about 1.41 times as long as one of its sides. As a result if the side of a square-
cover was lined up with the diagonal of the hole, it would slide through in spite of its lip.