1.         Significant Figures

 

What are significant figures?

 

They are digits that are obtained or meaningfully derived from a measurement. They include the single estimated figure that is part of every measurement. For example suppose that you weigh some sodium chloride. The electronic balance reads 2.0 g. It’s important that you record the mass as 2.0 g. The balance is telling you (at the very best; the uncertainty can be even greater.) that the actual mass is anywhere between 1.95 and 2.04 grams. But if you record 2g, you are telling your reader that the mass lies anywhere between 1.5 and 2.4 grams: an injustice to the balance!

 

When performing calculations, significant figures must also be respected. For instance if the 2.0 g of NaCl is dissolved in 60.0 mL of water, the calculator yields a concentration of 2.0/0.060 L = 33.3333333g /L. Where do you round off? The correct answer is 33g/L.

When dividing or multiplying, the answer must have as many significant figures as contained in the original measurement with the least number of significant figures.

 

Not convinced? Remember when we measure 2.0, we don’t know what the third decimal really is. Similarly, for 60.0 mL the actual volume may be anywhere from 59.95 to 60.04. So let’s look at some possibilities.

 

 

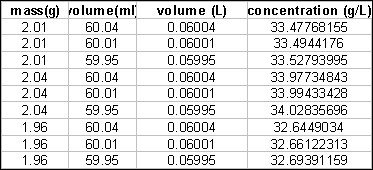
The results range from 32.6 to 34.0. Clearly the decimal place is meaningless. 33 g/L is the answer that reflects the accuracy of our measurements.

 

Rules for Determining Significant Figures.

1.                  All non-zero digits are significant. In any measurement, the last significant figure is an estimate but is still significant.

Example

Number of Significant Figures

2365

4

1.3365

5

11

2

 

2.                  Leading zeros (0’s before the nonzero digits) are NOT significant.

Examples

Number of Significant Figures

0.005333

4

0.3

1

0.000010

2

If you find this illogical, remember that the above numbers can be converted into scientific notation. For example 0.3 = 3 X10-1 has one significant figure.

 

3.                  Captive zeros (those between nonzero digits) are significant.

 

Examples

Number of Significant Figures

0.005003

4

0.301

3

3005

4

 

4.                  Trailing zeros (those after nonzero digits) are significant only if the measurement contains a decimal.

 

Examples

Number of Significant Figures

50000

1

50000.

5

7.000

4

 

5.                  Exact numbers and irrational numbers have an infinite number of significant numbers.

 

Examples

Number of Significant Figures

p

infinite

The 2 in C = 2 pr

infinite

3 people

infinite

 

6.         After carrying out a multiplication or division, the answer must have as many significant figures as contained in the original measurement with the least number of significant figures.

 

Examples

Answer

Number of Sig Figs in Answer

100./25

4.0

2

622.3 *3.5

2.2 X 103

2

3.65 per 4 people

0.91 per person

2 ( note the 2 people have an infinite number of sig figs and do not act as the limiting measurement

 

7.         For adding and subtracting, the answer must have the same number of decimal places as the least precise measurement

( the one with the least decimal places.)

 

Examples

Answer

23.91 + 11.999

35.91

11110.2 + .1333

11110.3

 

 

 

Important:      The rules for significant figures should be applied only to the final answer. That implies that all decimal places should be retained in the middle of a calculation.

 
 
 

 

 

 

 


8.         When taking the logarithm of a number, the answer gains a significant figure. Conversely when a measurement is applied as an exponent, the answer loses a significant figure. The reason is that in the latter case there is a greater propagation of error due to the exponent.

 

Examples

Answer

pH = -log(0.045)

pH =1.35

10-6.34 =

4.6 X 10-7

 

Note that for a pH measurement of 6.34 +/- 0.01, an value of 6.33 leads to a concentration of 4.68 X 10-7 whereas 4.57 X 10-7

The third figure is clearly meaningless

 

 

 

 

 

Siginificant Figures Exercise

 

 

1.         What is the correct number of significant figures in the following measurements?

 

a.                   2.0004 cm

b.                  300. cm            (there is a deliberate point after the last zero)

c.                   300 m

d.                  There are about 6 billion people on earth.

e.                   1.9900 ml

f.                      2.00 X 104 kg

 

2.         The mass of an empty can is 61 grams. Then 30 grams of water are added to the can. What is the lowest possible total mass for the can and water? The highest?

 

3.         A student observed that the temperature of 100.0 ml of water with a known density of 1.0 g/ml increased from 10.5 oC to 22.8 oC. Express the amount of heat absorbed by the water in kJ with the correct number of significant figures. Use c = 4.19 J/(goC).

 

4.         A gas sample contains 0.233 moles of He and 0.35 moles of H2. What is the total number of moles of gas in the sample, expressed with the correct number of sig- figs?

 

5.         H2 with a molar mass of  2(1.0797) g/mole consumes 8.0 grams of sodium, according to the following reaction:

 

2 Na (s)             +          H2(g)       à                    2 NaH(s)

 

How many grams of sodium hydride, NaH will be produced? Express with the correct number of significant figures.

 

6.         The initial concentration of ozone, O3 is 5.0 moles/L.  If the equilibrium concentration of oxygen is 3.0 moles/L, what is the value of K, expressed with the correct number of sig figs?

 

7.         In a lab, our measurements for the height of a tube ranged from 5.5 cm to 6.8 cm. The least accurate concentrations of the solutions used was 0.0010 M. Assuming that the value for K( an equilibrium constant) should have been expressed with just as many significant figures as in the above numbers, how should Peter have expressed the average of the following 4 values for K?

 

96.37754

87.05914

126.1661

230.3015