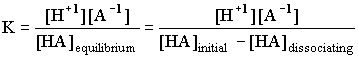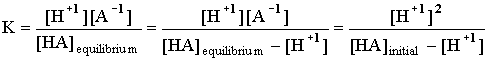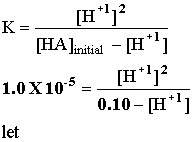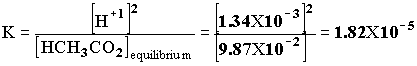|
|
|
Dissociation Constants for Weak Acids
Exercises
A weak acid is one with a reasonably small K, which implies that only a small percent of the acid is actually dissociating into H+ and a negative ion. For HA(aq) = H+(aq) + A -1(aq)
In all the examples we will see there will only be one H+1 coming out of the acid at any one time, so the ratio of [HA]dissociating into [H+1] will be 1:1, and the ratio of [H+1] to [A -1] will be 1:1. The above expression then becomes:
KA is an indicator of how strong an acid is compared to a
different acid. If KA is very large there is 1 mole of H+
for every initial mole of HX. So a 0.10 M solution will have a pH of 1. If KA
is low, the acid is said to be weak and an initial concentration identical to
the above will lead to a higher pH. Note the wording in the following:
Example 1: If Ka for the acid HA is 1.00 X 10-5, what is the pH of an acid with an initial concentration of 0.100 M? HA(aq) = H+1(aq) + A -1(aq).
Let x = [H+1] and cross multiply: x2 = 1.00 X 10-6 -
1.00 X 10-5x x2 + 1.00 X 10-5 x - 1.00 X 10-6 = 0. x = [H+1] = 9.95 X 10 -4. pH = -log[H+1] = -log[9.95 X 10 -4] = 3.00 Example 2 A 0.100 mol/L solution of HCH3CO2 is partially ionized. At equilibrium [H+1] = 1.34 X 10-3. Calculate the equilibrium constant of acetic acid, given: HCH3CO2(aq)--> H+1(aq) + CH3CO2 -1(aq).
|
B. KB
KB = dissociation constant for a base. Handle all Kb problems as if they were KA problems, except that they relate to bases, not acids.
Example 1 If the equilibrium concentration of XOH is 0.10 M, and the pOH = 3.0, what is the KB of XOH?
(First write an equation)
|
|
XOH(aq) = |
X+(aq) |
OH-(aq) |
|
I |
|
0 |
0 |
|
C |
|
1:1 ratio, so also 10-3.0 |
10-3.0 |
|
E |
0.10 |
0+ 10-3.0 =10-3.0 |
10-pOH = 10-3.0 |
KB= ![]() 1.0 X 10-5
1.0 X 10-5
|
Example
2 A chemist dissolved 0.3 moles of cocaine (C17H21NO4) in a liter of solution and its pOHwas 2.35. First write an equation to show how it acts as a Bronsted-Lowry base in water, and then find Kb. |
Cocaine is a topical anesthetic that was used in eye and throat surgery in the 19th and early 20th centuries. But in the 1900’s it gained popularity as a recreational drug. Its highly addictive psychological properties often destroy people both financially and emotionally. |
Let C17H21NO4 = X
|
|
X(aq) + H2O(l) = |
X+(aq) |
OH-(aq) |
|
I |
0.3moles/1.0 L = 0.3 M |
0 |
0 |
|
C |
1:1 ratio, so also 10-2.35 |
1:1 ratio, so also 10-2.35 |
10-2.35 |
|
E |
0.3 -10-2.35 |
0+ 10-2.35=10-2.35 |
10-pOH = 10-2.35 |
KB= ![]() 7 X 10-5
7 X 10-5
|
A policeman brings you a white powder that might be morphine sulphate (molar mass 383.1 g/mole), a strong pain killer that is physiologically addictive. Its pKB is 6.10. If the pH of a 100.0 ml sample is 10.4, how many grams of the white powder should appear upon evaporating the water, if the sample is truly morphine sulfate? C17H21NO7S(aq)
+ H2O(l) =
C17H21NHO7S+(aq) + More
on morphine? Read: http://www.emsb.qc.ca/laurenhill/science/morphine.html |
|
pH = 10.4
pOH =14 – 10.4 = 3.6
pKb = 6.10
Kb = 10-6.10
|
|
C17H21NO7S(aq) + H2O(l) |
C17H21NHO7S+(aq) |
OH- aq) |
|
I |
x = y + 10-3.6 |
0 |
0 |
|
C |
1:1 ratio, so also 10-3.6 |
1:1 ratio, so also 10-3.6 |
10-3.6 |
|
E |
y |
0+ 10-2.35=10-3.6 |
10-pOH = 10-3.6 |
KB= ![]() 10-6.10
10-6.10
Y = ![]() =0.0794
moles /L
=0.0794
moles /L
0.0794 moles /L*0.100 L = 0.00794 moles
0.00794 moles* 383.1 g/mole = 3.0 g