Solutions to 2003 Monthly Questions

Solution to January 2003 Question of the Month The question was:


The two pictures were taken 24 hours apart.
We see the moon and a star-like object which is actually Venus. What's responsible for their different positions? Whose apparent motion is faster? In reality does that object also move faster in space?Why or why not?
Solution:It's the moon's apparent position in the sky that has moved faster than that of Venus.
Although in reality Venus moves around the sun 34 times faster than the moon moves around the earth,
the moon is 238 times closer to earth, hence the illusion that the moon is moving faster.
How do we know that Venus actually moves 34 times faster? Knowing the average Venus-Sun distance =
1.08 X 1011 metres, we can compute the length of the orbit
(approximately a circle, even though it's technically an ellipse). We then divide this circumference by
a Venusian year=224.7 days ( time for 1 revolution). Converting to metres per second(m/s), we obtain an average value of 35 000 m/s. Doing the same for the moon (at an avg. distance of 3.76X 108m from the earth), we obtain an avg. velocity of 1022 m/s, which is 34 times slower than Venus.


But why? The velocity at which Venus moves is determined mainly by the force between it and the massive sun. The moon's velocity is governed by the force of attraction between it and the earth. Using Newton's formula twice,F=Gm1m2/r2, where G = 6.67 X10-11Nm2/kg2,m1and m2are the two masses, and r is the distance between them, we can calculate that the Venus-Sun gravitational force is 263 times stronger than the Earth-moon one. Setting this ratio equal to the ratio of the centripetal forces ( Fc = mv2/r)of the two bodies, we confirm that the ratio of Venus's velocity to that of the moon is indeed 34.
Solution to February 2003 Question of the
Month The question was:
Around 1913, two scientists at New York University found that the density of water, which they measured to several decimal places, varied from sample to sample. They erroneously concluded that at constant temperature water's density is not unique. What were they unaware of?
Reference: John S. Ridgen, Hydrogen: The Essential Element,Harvard University Press, 2002
Solution:
Water can contain deuterium, an isotope of hydrogen with one extra neutron. 2H will raise the density of water, but its percentage varies from sample to sample.
Another Hydrogen Question
Solution to March 2003 Question of the Month
The question was:
Tritium, 3H, is an isotope of hydrogen. Imagine a 220 g glass of water with each H2O molecule consisting of 1 oxygen atom and two tritium atoms instead of hydrogens. You accidentally empty this glass of radioactive water into the ocean.
Six years later half of the tritium is no longer radioactive, and meanwhile your water has mixed perfectly with the rest of the water in all of the earth's oceans. With a glass, you scoop up 220 g of water at a beach. How many radioactive water molecules will be in your glass? You'll need the following data:
| OCEAN | DEPTH(meters) | AREA(km2) | VOLUME(L) |
| Pacific | 4188 |
1.65 X108 | ??? |
| Atlantic | 3735 | 8.17 X 10 7 | ??? |
| Indian | 3872 | 2.84 X 107 | ??? |
| Arctic | 1038 | 3.66X 106 | ??? |
Solution:
First we need to obtain an estimate for the total amount of water in all of the earth's oceans. For each ocean,convert the area to m2 by multiplying km2 by 10002. Multiplying the result by average depth, we will obtain volume in m3.
To get litres we multiply by 1000. Add them all up and we get 1.11 X1021L in all of the earth's oceans.
A 220g glass of water from the beach is about 220ml = 0.220 L. This represents a small fraction of the entire volume found in the earth's oceans. It equals 0.220/1.11 X 1021. If we then multiply this fraction by the number of tritium-labeled water molecules,
we will know how many are in that glass. Originally we dumped 220g/(22 g/mole) [note with tritium,
the molar mass of water gets heavier]= 10 moles = 6.02 X 1024 molecules. But tritium is radioactive
so only half of those molecules remain = 3.01 X 1024 molecules.
Answer = 0.220/1.11 X 1021*3.01 X 1024 molecules = about 600.
This adds one more reason to why we study moles. Moles help us realize
how our bodies constantly borrow molecules from the planet and then return them.
Each time perspiration escapes from your skin,
because of the water cycle and of the extreme smallness of molecules, a minute amount of
water that flowed through your veins and partially filled your lungs end up in the tissues
of all other people, plants and animals on the planet.
Solution to April 2003 Question of the Month The question was:
My daughter complains if I pick her up too early from her after-school program, so I've had the chance to measure my tire pressure frequently.
- On a cold day in February (-20oC), the tire pressure was 35 psi (pounds per square inch; can be treated like kPa in Gay-Lussac's Law)
- Thirty days later, the air temperature is now 10oC.
- Assume that the rate of change of temperature with respect to time is linear(constant)
- With time my tires lose air at an average rate of 0.083 psi/day.
a.Find the overall rate at which tire pressure changes with time in psi/day.
b.If the optimum tire pressure for my specific tires is 35 psi, should I let some air out or increase the pressure (now,30 days later)
Solution:
a. overall rate = (rate at which pressure changes with temperature)*(rate at which temperature changes with time) - (rate at which pressure changes with time due to leakage)
Use Gay Lussac to obtain the pressure at 10 C.
P2 = (T2/T1)P1 = (283/253)(35) = 39.2 psi.
rate at which pressure changes with temperature=( P2 - P1 )/T2 - T1)= (39.2-35)/(283K-253 K) = 0.14 psi/day - 0.083 psi/day = 0.057 psi/day
b. Tire pressure should be released since it should have increased to 35 + 0.057 psi/day(30 days) =36.7 psi.
Solution to May 2003 Question of the Month The question was:
How do you find the mass of a little cup of water without a balance or any kind of volume-measuring device?
Solution:
If you place the cup in a calorimeter, you could attach it to a power source. Knowing the duration in seconds for which the calorimeter was connected, the voltage, and current, we can calculate the amount of energy absorbed by the water in the calorimeter using E = VIt. If we also keep track of water's initial and final temperature, with c = 4.19 J/(gC) and with Q= mc Dt, we can calculate m, the mass of water. Note we assume that Q = E, which is approximately true.
Solution to June 2003 Question of the MonthThe question was:
Wine
is 12% alcohol by volume, meaning that a 100 mL glass contains 12 mL of alcohol
and approximately 88 mL of water. In such a glass of wine, how many molecules of
water are there for every molecule of alcohol, C2H6O? (The
density of alcohol = 0.80 g/ml)
Solution:
The
ratio of molecules is not proportional to the ratio of volumes. Using densities,
convert the volumes to mass. 12 ml of C2H6O = 12*0.80
= 9.6 g; 88 *1.00 = 88 g of
water; Finally convert to moles by dividing by molar mass, and the ratio of
moles is the ratio of molecules: [88/18]/[9.6/46] = 23: 1.
So although wine is 12% alcohol by volume, only 1/(23+1)= 4% of wine's molecules are ethanol,
which might give some people an excuse to drink more!
Solution to July 2003 Question of the Month
The question was:
One morning I woke up with a rash on my ears, cheeks, arms and belly.
In fact, my ears were so swollen that I looked too funny for school.
So I went to the hospital, where I was scolded for showing up at the
emergency ward for such a non life-threatening condition.
The doctor treated me nevertheless, claiming that my affliction was either
viral or an allergy. Just in case it was the latter, he prescribed something,
which turned out was not the drug of choice for such a rash.
I found that out from a dermatologist, who according to my family doctor was the best in town. You see, the medication had not helped me at all, and two days later I was still uncomfortable and looking as though I had been beaten up.
The dermatologist said it looked like a contact dermatitis,
which is an allergic reaction to something you touch. He went through a list of possibilities but said that it was up to me to figure out the exact nature of the allergen. He sent me home with the puzzle and a prescription for a cortisone gel that would alleviate the symptoms until I figured out the cause of the irritation.
The next morning when I put on my underwear,
I felt an itch in a new place, and I realized out what I was allergic to.
What was my hypothesis, and what did I do to verify it?
Solution:
The new underwear was from a new batch of laundry.
Since I had not experienced any irritation from previous batches,
I asked my wife if she had recently switched detergents.
Sure enough, she had. We then went through the very tedious task of rewashing
everything with the old detergent, and my rash never returned.
The soap residues on my bed sheets and pillow cases especially were the
reason my ears, cheeks, arms and belly had been the most affected.
(I had slept without a pyjama top)
Solution to August 2003 Question of the Month
The question was:
A student was hoping to find the percentage of oxalates, C2O4-2, in Earl Grey tea.
He first weighed 2.14 g of the tea and then added 200 ml of boiling water. After four minutes, he added 100.0 ml of 1.5 g/L Ca(OH)2 to the sample, expecting the following to happen:
Ca(OH)2 + C2O4-2 --> 2 OH-1(aq) + CaC2O4(s)
He waited a while, saw lot of brown precipitate forming and filtered the mixture. After a few days, the residue on the paper was totally dry, and after subtracting the mass of the filter paper, he found the mass of the solid to be 0.52 g.
The student then erroneously concluded that the tea consisted of
0.52g*(88g of C2O4-2 / 128 g of CaC2O4(s))/ 2.14g = 17 % oxalates.
Judging from the data given in the question, is there a possibility that the 0.52 g of solid included more than just calcium oxalate?
Solution:
Since only 100.0 ml of 1.5 g/L Ca(OH)2 had been used,
(a total of 0.100 L [1.5g/L][mole/74g] = 0.0020 moles),
from the equation, we see that the maximum amount of CaC2O4(s) that can
be produced from this is 0.0020 moles*128 g/mole = 0.26 g.
Because the student produced twice that much residue,
half the impurities are definitely not CaC2O4(s),
and there is a strong possibility that the rest of the residue
that precipitated at the high pH may not even contain oxalates.
Solution to September 2003 Question of the Month
The question was:
If you have not yet tackled a challenging project, you may not realize how important persistence and serendipity can be in scientific discoveries. Here is a problem which, although is more mathematical than scientific, will give you a taste of this important truth.
22/7 is a 2 decimal approximation to p. Suppose that you want to discover some fractions that are at least 11 decimal approximations of this useful irrational number. To avoid trivial solutions, you can't merely look up p, move the decimal, divide by a power of 10 and reduce. Your tool: the TI-83 calculator, which most of you have, and suppose that other people on the trail seem to think that the "FRAC" function under the MATH menu is a good starting point. This function converts decimals like 0.222222222…into fractions, for example, to 2/9 if you simply press 0.222222222… followed by "MATH"
and "FRAC". Good luck, and don't give up so easily, because in all likelihood a successful
find will depend on serendipity and persistence.
Solution:
Try p FRAC and the calculator will fail to give you a fraction. As an alternative,
suppose you attempted to pick an arbitrary value for the radius of a circle and asked the calculator for the area in FRAC form. Potentially, you could then work backwards and express p as a fraction. Try that, and you will not succeed.
At this point, you may feel that the approach seems flawed, and there every reason to
abandon it, but being persistent you try obtaining the volume of a sphere in FRAC form:
(4/3) p r3 FRAC. For values of r up to 7, the calculator keeps yielding
decimals, but for r = 8, we obtain, 8580787/4001. By multiplying
this fraction by ¾ and dividing by 83,
( treat the numerator and denominator separately), you will get 25742361/8194048,
which is an accurate representation of p to 11 decimal places.
The table below reveals what fractions are revealed by r values of 8 to 12.
| r |
p(3.14159265358979...) Approximation |
| 8 |
25742361 / 8194048 = 3.14159265359441 |
| 9 |
8858575 / 2819772 = 3.14159265359043 |
| 10 |
87750966 / 27932000 = 43875483/13966000 = 3.14159265358728 |
| 11 |
149345019 / 47537996 = 3.14159265359019 |
A few years ago I contacted Texas Instruments to ask them why their calculator acted that way, but nobody could give me an answer. Until an answer surfaces, consider it a fluke.
Solution to October 2003 Question of the Month
We were recently visited by a
salesman who tried to sell us a water filtration system. He had a metal brief
case full of chemicals, so naturally I looked forward to his presentation.
By means of
a precipitation reaction, he first demonstrated that our tap water contained a
certain degree of hardness caused by magnesium (Mg+2) and calcium (Ca+2)
ions. All natural water contains those ions to some varying degree. Our water
had 120 ppm of the stuff, which is equivalent to about 120 mg of ions for every
litre of water. These ions interfere with the action of soap. To demonstrate
this he filled an Erlenmeyer flask with 120 ml of my tap water and a second
flask with the same volume of tap water filtered with a resin-containing column
that he pulled out of his metal brief case. The resin exchanges sodium ions for
Mg+2 and Ca+2, which bind to a negative ion on the resin
(SO3-2), effectively softening the water. Each sample
then received 5 drops of his soap. The softened water and soap, upon mixing,
created a persistent foam, whereas tap water and his soap produced only a
fraction of foam. Moreover, the foam quickly subsided, and the remaining
solution was mirkier than the one at the bottom of the softened water.
(1)
What happened at the molecular level during his soap
demonstration?
(2)
Why was his demonstration misleading and not entirely relevant
to everyday washing?
(3)
Why is removing Ca+2 and Mg+2 from tap
water not necessarily a good idea?
Solution:
(1) Bar soap and liquid hand soap often contain a
mixture of sodium stearate (C18H35O2Na) and
sodium palmitate. Unfortunately, in the presence of either calcium or magnesium
ions, stearate and palmitate will form precipitates, which no longer act as
soap molecules. For example:
2 C18H35O2Na(aq)
+ Ca+2(aq) -->
2 Na+1(aq) + Ca(C18H35O2)2
(s)
When either the stearate or
palmitate were added to the treated water, there was no calcium to interfere
with the soap ions.
(2)
His presentation falsely suggested that all soaps are alike.
In reality, detergents contain either sodium alkylbenzenesulfonate, which in
the presence of Ca+2 and Mg+2, does not
precipitate to the same extent as bar soap. Older types of detergents contain
phosphates, which will “fish out” the problematic calcium and magnesium ions
(by forming insoluble magnesium or calcium phosphate). After some dubious
excuses, the salesman agreed to repeat his experiment with my own detergent,
and the differences were far less dramatic. There was only slightly less foam
produced when the detergent was added to my untreated tap water.
(3)
Drinking water should not be free of Ca+2 and Mg+2. Both of these are essential ions for
the human body. Calcium ions are needed for bone formation and teeth. It also
plays a role in blood clotting, muscle contraction and relaxation, nerve
transmission, and enzyme(ATPase) activation. Magnesium is also needed for bones
and teeth. It is a coenzyme in carbohydrate and protein metabolism and helps
nerves and muscles function.
Solution to November 2003 Question of the Month
The question was:
In
the July 2003 column Microcosm of The Globe and Mail, the author
had argued that there are at least 70 sextillion stars in the universe ( 1
sextillion = 1021), but that number is merely the number of molecules
found in a raindrop. Mel Schriver,a chemistry professor, wrote back claiming
that the number of stars is more like the number of molecules in seven to 10
raindrops. Do you agree?
Solution:
70 X 1021 molecules/(6.02 X 1023molecules/mole)*(18g/mole)
translates to 2.1 g, almost half a teaspoon of water, so certainly
Schriver is correct in stating that 2.1 g is more like 7 to 10 raindrops,
not one.
Extra
At the time of writing, the Red Sox had a shot at the pennant, so my
enthusiasm for baseball had not yet waned for the season. As most baseball fans
know, batting average is simply the ratio of the number of hits to the number at
bats. That makes it a linear relationship: for any given number of at bats, a
.400 hitter (hypothetically, since there has not been one since Red Sox slugger
Ted Williams did it about sixty years ago)will have obtained twice the number of
hits as a .200 hitter. But consider a similar statistic known as the batting
average of a pitcher's opponents. Strange as it may seem, if you plot the
number of hits given up by the pitcher per game versus the opponents' average,
you will notice a non-linear relationship! Can you show why?
Solution
Let A = batting average for opposing hitters
y = number of hits allowed per game
P = average innings pitched per game
E = average team errors per game
A = hits/at bats = y/ (y + E + 3P)
3P because a pitcher has to retire 3 batters to get credited with 1 inning
pitched)
Solving for y:
y = A (E + 3P)/(1-A)
For a starting pitcher who averages 7 innings per game and whose team
averages 1 error per game:
y = 22A/(1-A). I plotted opponents' averages ranging from 0.175 to 0.400:
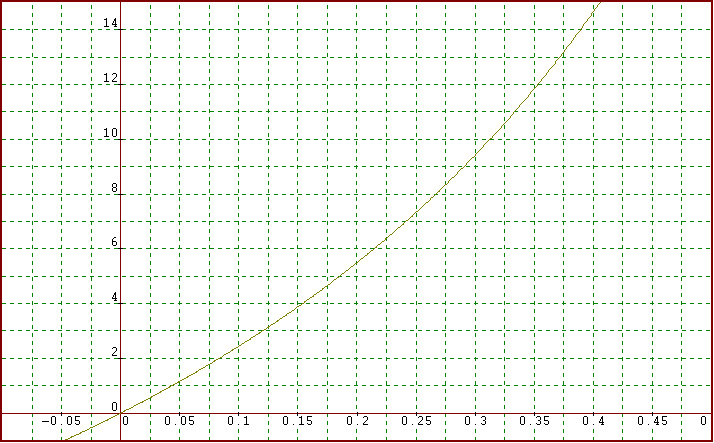
So a pitcher whose opponents average only .200(like
Pedro Martinez) only gives up about 5.5 hits per game, but a pitcher whose
opponents average .300 does not give up 1.5 times the number of hits(which would be about 8.25) but over
9.5 hits!
Solution to December 2003 Question of the Month
The question was:
As an airplane gains altitude, it flies through air that is not as compressed by gravity,
in other words, it moves through air of lower density. Changing temperatures and humudity also affect density on the runway. Consider what this does to
(1) the plane's lifting power,
(2) to the friction it encounters,
(3) and to how well its engines can function,
and decide whether lower air density is an advantage or disadvantage to an aircraft.
Solution:
Although a lower density of air would reduce drag(air friction), factors (1) and (3) make flying more difficult
See this article. With less molecules around, not as many can be deflected underneath
the plane by its curved wings and fuselage, so there is less lift generated. A lower air density also means less
oxygen for its engines. This isn't just theory. Consider that a Cessna needs only 224 m for
takeoff at 10o C, but it requires 268 m at 35o C(source: Cessna's pilot's operating handbook (POH))
Why does a higher humidity content lower the density of air? Air is always a mixture of gases. Each component of a gas mixture contributes to a partial pressure.
Air containing moisture decreases the partial pressure of the dry air component(oxygen, nitrogen, argon, carbon dioxide). In simpler terms,
the moisture molecules (H2O)are displacing some of the dry air molecules. But H2O has a molar mass of only 18g/mole whereas dry air
has a higher average of about 29 g/mole. Calculating the density of moist air is further complicated by the fact that
water vapour molecules do not act as an ideal gas.
The following formula takes all of the above into account. It basically comes from a fairly thorough explanation found
at http://wahiduddin.net/calc/density_altitude.htm.
What I've done is simply plugged in the different specific gas constants for dry and moist air, and modified it so that
it is compatible with kPa and K units.
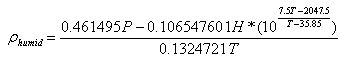 rhumid
rhumid= density of humid air in kg/m
3 = g/L
H = relative humidity in decimal form
T = air temperature in Kelvin(K)
P = atmospheric pressure in kilopascals(kPa)
Page Maintained by E. Uva;
euva@retired.ca
Copyright ©2007
Created:April/6/1996;