Solutions to 2008 Monthly Questions

Solution to January 2008 Question of the Month
The question was:
From which hemisphere was this photo taken? To answer the question, you do not need to
recognize the specific desert photographed. You just have to analyze one of the details in the picture.

Solution:

Mare Crisium on the moon is always between the 12 and 6 o'clock position when the moon is viewed from the Northern Hemisphere.
But here it is in the 8 o'clock position, so it must be a Southern Hemisphere photo. In fact it was taken from
the Namib Desert in Namibia, Africa at a latitude of 24 oS. They are seeing the moon inverted because they are
"at the bottom of the world", from our perspective. For moon pictures taken from various parts of the world, click here.
Solution to February 2008 Question of the Month
The question was:
Fermi problems are estimation problems based on reasonable assumptions.
At first a Fermi problem seems to be a piece of trivia unrelated to logic,
but with a little thinking and basic knowledge, an estimate within the right order
of magnitude is easily attainable.
Here's an example: How many high school chemistry teachers work in Canada?
Solution:
First we need to estimate the number of high school students in Canada.
In most provinces children are in high school from the ages of 12 to 18,
for a total of six years. The average life expectancy is close to 80 years and Canada's population is about 33 million. Because of demographics, the age-distribution is skewed away from the adolescent years, but roughly there are about (6/80)(32 X106) = 2.4 million Canadians in high school.*
There are roughly 18 students for every high school teacher,
and if I use the high schools I know as examples there are either 1 or 2 chemistry teachers (call it 1.5)for every 80 high school teachers.
So there are 2.4 million students(1 teacher /18 students) (1.5 chem teachers /80 teachers) = 2500.
Given that a few of our estimates involved only one significant figure, we would have to conclude that there are somewhere between 2 000 and 3 000 chemistry teachers working in Canada.
*How good is this type of reasoning?
Well, according to Census Canada, there were 31,612,895 Canadians aged between 0 and 80 in 2006. Stats Canada
(at http://www12.statcan.ca/english/census06/data/highlights/agesex/pages/Page.cfm?Lang=E&Geo=PR&Code=01&Table=1&Data=Count&Sex=1&StartRec=1&Sort=2&Display=Page) ) does not give the actual number of children aged between 12 and 18, but they do have the "0 to 14" figure. According to the way we came up with our estimate we would guess that there should be about (14/80)( 31,612,895) = 5 532 257 children in that age group. The actual number is 5,579,835, a difference of less than 1%!
Solution to March 2008 Question of the Month
The question was:
There are 21 parts of oxygen per 100 parts of atmosphere, but only 377* parts of carbon dioxide per million.
In 1850 there were only 286 ppm of CO2(ice core data). Let's just say that
on average approximately 1.5 moles of oxygen are consumed for every mole of carbon dioxide introduced.
What percent
of oxygen have we removed from the atmosphere since 1850?
*(2004 measurement = http://cdiac.ornl.gov/ftp/trends/co2/maunaloa.co2)
** Expectedly, we continue to eat up a small percentage of oxygen. CSIRO scientists have measured a small decline
in oxygen between 1980 and 2000, the longest period over which such an assessment has been made.
Solution:
Proportionally for every 106 molecules of air there are 210 000 parts of oxygen.
In 1850 there were only 286 ppm of CO2 ; now there are 377.
This represents an extra 91 molecules of CO2 for every 106 in the atmosphere.
Stoichimetrically, 1.5 * 91 = 136 molecules of oxygen are consumed for every million.
136/210 000 * 100% = 0.065% loss
Solution to April 2008 Question of the Month
The question was:
Do you know the answer to this poetic couplet?
|
Why is it that ice is more dense than snow
|
|
If both are solid forms of H2O?
|

|
Solution:
Ice's density varies from 0.850 g/cm3 to 0.920 g/cm3.
Fresh snow's density varies from only 0.050 g/cm3 to 0.150 g/cm3.
Snow with dendrites allows more air to fit in between crystals, lowering the density.
If snow flakes are in the shape of simple needles or column-like structures, less air fits in between.
But in general, compared to ice, snow contains a greater amount of air , which is why an equal volume of ice is heavier.
In between snow and ice are névé and firn. Névé is partially melted, refrozen and compacted snow.
If it survives another season, its density increases from 0.50 g/cm3 to over 0.55 g/cm3.
At that point it becomes firn, which, with pressure, will become glacial ice. Then you have a glacier.
References:
http://www.physicalgeography.net/fundamentals/10ae.html
http://snowcrystals.com
Solution to May 2008 Question of the Month
The question was:
At the end of the earth's Paleozoic Era, about a quarter of a billion years(2.48 X108) ago, 90% of life on earth was wiped out.
Yet the era left us with more than just fossils. Most of the world's coal and limestone(from which we get lime to make cement)
was produced in the Paleozoic Era.
If you reduce the entire earth's history to a calendar year, with January 1st, 12 AM, being the formation of the earth, on what date does the Paleozoic Era End?
Solution:
The earth is 4.55 billion years old, and the cataclysmic end of the Era occurred 0.248 billion years ago.
If we express that as a fraction of the whole, we get (0.248 X109/4.55 X109)*365= 19.9 days ago = Dec 12th, (0.1*24=2.4 hours),2:24 AM. Keep in mind that
on the Earth calendar our present time is considered to be Dec 31, 12 PM, on the verge of beginning day # 366.
see Calendar Earth
Solution to June 2008 Question of the Month
The question was:
The Tunguska Event occurred on June 30th, 1908
(close to 100 years ago, at the time of writing) in Siberia,
north of Western Mongolia. Estimates of the energy of the blast were probably
in the 10-20 megatons-range, about 1000 times as powerful as the bomb dropped on Hiroshima,
Japan . The explosion knocked over an estimated 80 million trees over 2,150 square kilometres
(830 square miles). The earthquake from the blast measured 5.0 on the Richter scale.
Forty kilometres from the center of the explosion, people felt the heat,
watched windows shatter and were knocked off their feet.
Of course, the event occurred three decades before nuclear weapons were discovered,
about half a century before the first satellite went into orbit, and in the same year that
the first two-passenger flight was made.
What caused the blast? Can you form a hypothesis? What kind of evidence would support
your hypothesis?
Hints:
Expeditions sent to the area in the 1950s and 1960s found microscopic glass spheres in siftings of the soil. Chemical analysis showed that the spheres contained high proportions of nickel and iridium.
Soviet experiments performed in the mid-1960s, with matchstick models and small explosive charges slid downward on wires, produced butterfly-shaped blast patterns strikingly similar to the pattern found at the Tunguska site. The experiments suggested that the object had exploded in mid-air.
A University of Bologna investigation(2007) of Lake Cheko in the once devastated area has led to surprising results. The lake bottom's geology reveals a funnel-like shape not seen in neighbouring bodies of water.
This summer(2008) the same researchers are returning to look for a metallic fragment that could have been a leftover of an asteroid that exploded in the air over the epicenter.
References:
BBC News http://news.bbc.co.uk/2/hi/science/nature/6239334.stm
Wikipedia http://en.wikipedia.org/wiki/Tunguska_event
Scientific American June 2008 http://www.sciam.com/article.cfm?id=the-tunguska-mystery&sc=rss |
 |
Solution to July 2008 Question of the Month
The question was:
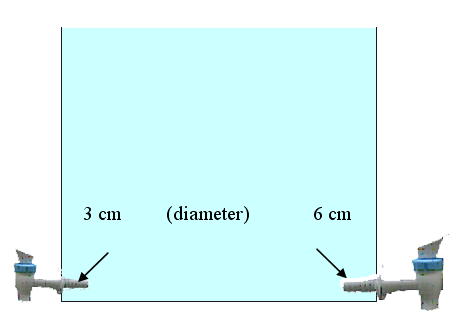
When only the small tap is opened, it takes the water tank 16 minutes to empty out.
How long will it take for the tank to drain when both taps are opened,
if the large tap is twice as wide as the smaller one?Solution:
Let V = volume of water in the tank.
The outflow rate for small tap = V/(16 min).
If the other tap has twice the diameter, then the pipe will have 4 times the cross sectional area. This implies 4 times
as much water will flow out of the larger tap per unit of time.
If it took the other tank 16 minutes to empty out, on its own, the large tap would empty the tank in
16/4 = 4 minutes.
Its outflow rate = V/(4 min).
But both taps are turned on, so the rates are additive:
Total rate = V/16 + V/4 = 5V/(16 min).
Time = volume/rate = V/[5V/(16 min)] = 16/5 = 3.2 minutes.
For more mathematics of pipe flow see
pipeflowcalculations.com
Solution to August 2008 Question of the Month
The question was:
Doing a backwash for your pool not only cleans the filter but it also prevents the buildup of calcium ions, which can not only irritate swimmers but could lead to troublesome deposits.
Of course we are assuming that you are treating your pool with calcium hypochlorite, Ca(ClO)2) . There are other methods of eliminating bacteria and algae, but some of these alternatives can lead to other problems.
Here's the question:
Over two pool seasons (38 weeks), you added 15.9 kg of Ca(ClO) )2 to a 44 000 L pool. After the first season, you emptied out 3/8 of the pool, and every two weeks during pool season you performed a backwash, which reduced the water level to 46/48 th of the original. You subsequently filled up with fresh water again to get the pool water back to its original level.
After 38 weeks of use, what was the concentration of Ca+2 in mg/L? (Recommended levels are 250 -350 mg/L.)
Solution:
40 g/mole = molar mass of Ca+2
40+71+32 = 143 g/mole = molar mass of Ca(ClO) )2
5/8 = remaining amount of water after removing 3/8
Frequency of backwashed = 1 per 2 weeks
Remaining calcium in kg = 15.9 kg(40/143)(5/8)(46/48)(38/2) = 1.238 kg
Concentration = 1.238 kg (106mg/kg)/44000L = 28.1 mg/L, which is below the recommended level of calcium ion, but that's ignoring what is already in the tap water. The 28.1 mg/L just represents what is added to the background amount.
(Thanks to Nadine Brückmann (brueckmn@uni-duesseldorf.de), who pointed out a calculation error in the original post.)
Extra Pool Problem
It is not unusual for pool water levels to drop by a quarter to half an inch per day.
On a hot windy day in July, I measured a drop of 0.75 cm in a 42 000 L pool (water height = 120 cm) over a period of 20 hours.
How does this compare to the evaporation in California Part Lakes,
which averaged a loss of 1250 m3 per day over an area of 0.2 km2?
Answer
First we calculate the surface area of the pool water from the amount of water lost.
42000 L (0.75 cm/120 cm) = 262.5 L lost
262.5 L = 262 500 cm3
262 500 cm3 /0.75 cm = 350 000 cm2
The rate of pool water lost expressed in L/m2/h = 262.5 L/(350 000 cm2*m2/1002cm2)/20 h = 0.37(5) L/m2/h.
Now we need to use the same units to express the rate of water lost from the California Part Lakes.
(1250m3*1000L/m3) /(24 h*0.2 km2*10002m2/km2) = 0.2(6) L/m2/h
An above ground pool is surrounded by metal so it is similar to a pan evaporation experiment used by farmers to predict evaporation rates.
According to Wikipedia, "evaporation from a natural body of water is usually at a lower rate because the body of water does not have metal sides that get hot with the sun.
Most textbooks suggest multiplying the pan evaporation by 0.75 to correct for this." If we apply the 0.75 factor
to 0.375, we obtain a very similar(identical if you take significant figures into account; see bracketed figures)rate of 0.28 L/m2/h
Solution to September 2008 Question of the Month
The question was:
Batteries are not always the best thing for our pocket books or the environment. In 2007, Canadians bought over half a billion non-rechargeable batteries and 25 million rechargeable ones.
Like many of the products we use, they are not well understood.
1) Are there rechargeable batteries that do not contain the toxic metal cadmium but which are also less expensive than lithium batteries?
2) How do batteries work in the first place?
3) Can AA batteries be used when a toy or flashlight requires C or D batteries?
4) Can AA batteries be used instead of the expensive CRV-3 battery required by some digital cameras?
5) If a toy needs new batteries, what can one do with them before recycling them, even if they are not rechargeable?
Solution:
1) and 2)A nickel-metal hydride battery, abbreviated NiMH, is a type of rechargeable battery similar to a nickel-cadmium (NiCd)
battery but instead of using cadmium at the cathode(where electrons are accepted),
it uses a hydrogen-absorbing alloy that forms the hydride.
H2O + M + e = OH- + MH,
where M is an intermetallic compound involving a combination of rare earths with nickel, manganese, cobalt or aluminum.
As in all batteries, if one chemical reaction accepts electrons as they are returned to the cell, there has to be a reaction that churns out electrons in the first place, and this is where the nickel comes in:
Ni(OH)2 + OH- = NiO(OH) + H2O + e
3) A plastic adaptor can accommodate AA batteries in a C or D slot. Rechargeable battery kits sometimes include these useful devices. AA, C and D batteries are all 1.5 V cells. Size does not matter; voltage does.
4) Some cameras can accommodate either one. If an older model does not, it's because the contact plate is missing for the AA batteries. But you can still get around this. To mimic the +/- arrangement on top of the CRV-3 battery,
flip one of the AA batteries nipple-down to match the negative part of the CRV-3. Then fold a piece of aluminum paper and place it at the bottom of the batteries in between them and the door of the battery inlet.(actually even my older Kodak included a contact plate;
I probably reversed the polarity on the batteries the first time I tried it, and I erroneously concluded that double AA batteries were not compatible.)
5) Use them somewhere else, like in a remote control or especially in a wireless mouse. Several gadgets do not need the full 1.5 volts to work.
Sources of information:
Stifung Gemeinsames Rucknahmesystem Batterien (GRS). March 2005.GRS Annual Report
Global Industry Analysts (GIA). June 2004. Consumer Batteries Report
Freedonia Group. May 2005. Batteries to 2009
Solution to October 2008 Question of the Month
The question was:
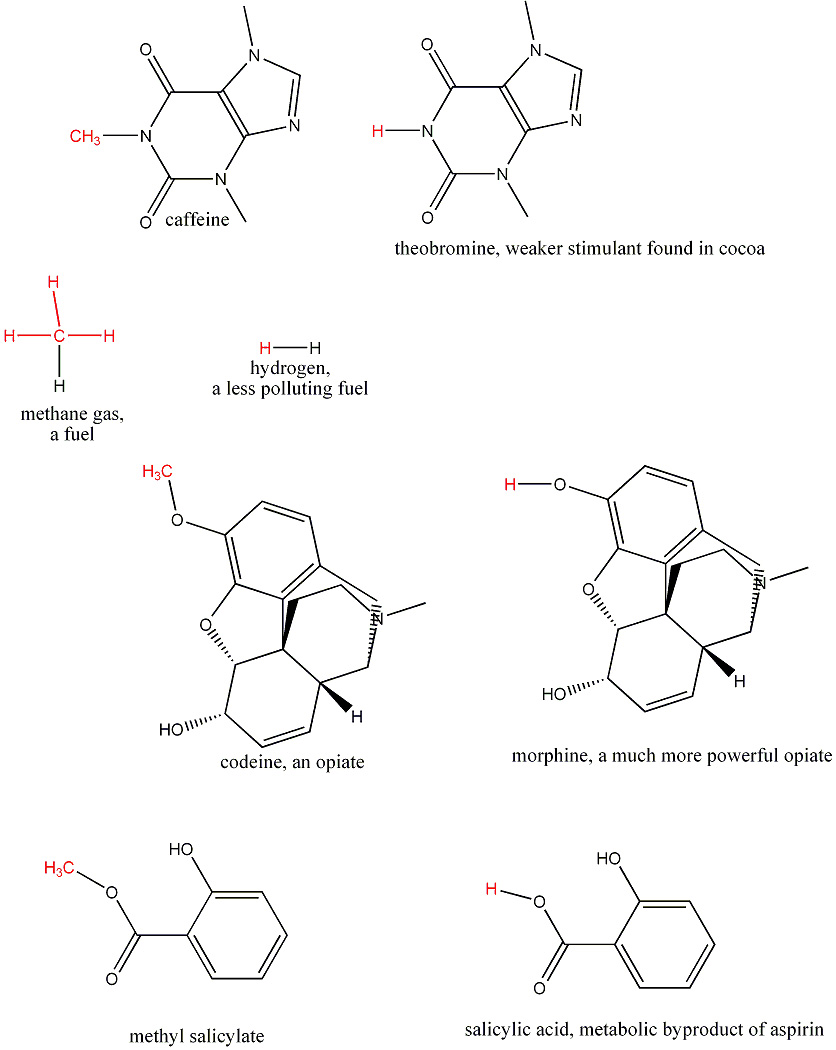
It does not take a radical alteration in structure to
change the properties of molecules.
Can you find examples of pairs of molecules that differ by only one carbon and two hydrogens?
For instance, if you replace a CH3 group in drinking alcohol(CH3CH2OH) by a single hydrogen, it becomes the poison wood alcohol CH3OH.
Solution:
Solution to November 2008 Question of the Month
The question was:
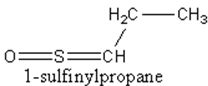
Onions contain amino acid sulfoxides.
Cutting an onion releases enzymes called allinases, which converts the amino acid sulfoxides
to sulfenic acids. The sulfenic acids, in turn, spontaneously rearrange to form 1-sulfinylpropane,
the chemical that gas that diffuses though the air, reaches the eyes and triggers tears.
But chilling an onion reduces the volatility of the lachrymator, so you are less likely to cry.
When we first got a dog and he experienced his first winter snow with us,
I imagined that the cold air would reduce the volatility of whatever made Blues so curious.
In addition, I thought the snow would act as a physical barrier between the ground and his nose.
But I was wrong. Why can dogs smell through snow?
Solution:
There are many air spaces between snow crystals, temporarily trapping smells.
When those surface, dogs pick them up.
Rescue dogs can search for the scent of human beings buried beneath up to 15 feet of snow.
When hydrogen peroxide(H2O2) was first made in 1818 from barium peroxide(BaO2), and for many years after, scientists were under the false impression that H2O2 was not stable. When they tried to separate it from the water that it was dissolved in, it would fizz and turn into more water. Interestingly, it was the same reaction that is familiar to us now when H2O2 is added to blood, battery powder or to a piece of potato.
Why was H2O2 decomposing?
Solution:
Strong acids are typically contaminated with metallic ions. These, like the MnO2 in battery powder or catalase in living tissue, act as catalysts in the breakdown of hydrogen peroxide.
Catalase is a very versatile biological catalyst because it not only breaks down hydrogen peroxide, but it can use hydrogen peroxide to get rid of alcohol, phenols and other chemicals.
Page Maintained by E.Uva
Comments:
euva@retired.ca or
euva@prof.emsb.qc.ca
Copyright ©2008