Solution:

His book is about mosquitoes, the vectors of

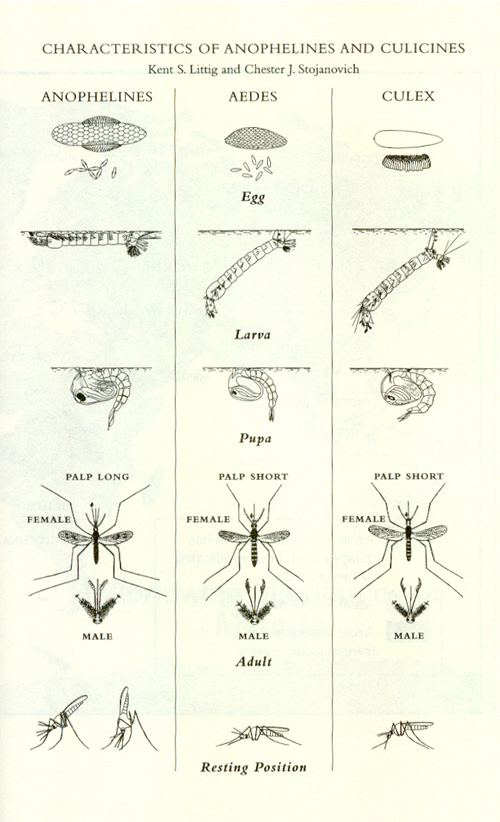
1. human malaria
2. dengue
3. yellow fever
4. West Nile virus
5. filariasis

(1) is transmitted by mosquitoes of the genus Anopheles. (2) and (3) are transmitted by the species Aedes aegypti. Culex pipiens, the common house mosquito, can transmit (4) and (5).

Malaria was once considered to be on the verge of being conquered. But in recent decades it has made a strong comeback due to pesticide resistance, poorly administered drugs and other factors. The author still feels that DDT should not have been banned as a pesticide. If applied thoroughly and over a short time span, it still provides an effective and less toxic means of controlling the mosquito population, which spreads Plasmodium ,the organism which actually causes malaria.



---

Solution to February 2002 Question of the Month

The question was:

Compare the following:

4 KNO₃ + 7 C +  S à   K₂CO₃ +   K₂S + 3 CO + 3 CO₂ + 2 N₂.

10KNO₃ + 16 C + 2 S à 3 K₂CO₃ + 2 K₂S + 5 CO + 8 CO₂ + 5 N₂.

The equations contain identical reactants and products. Both are balanced representations of what happens when gunpowder explodes. Yet they are not equivalent, in the sense that one equation has not been multiplied by a certain factor.

It turns out that there are practically countless ways by which you can balance the equation:

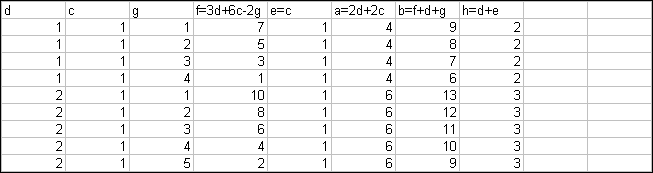
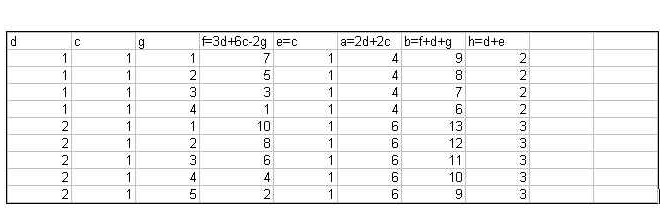
a KNO₃ + b C + c S à d K₂CO₃ + e K₂S + f CO + g CO₂ + h N₂.

Mathematically, why is this so?

Solution:

Each atom has to be balanced:

K:        a = 2d + 2e

N:        a = 2h

O         3a = 3d + f + 2g

C         b = d + f + g

S          c = e

Since c = e, then a = 2d+ 2c (see K)

Dividing the equation for oxygen by 3:

a = d + f/3 + 2g/3, which we can substitute in to the new equation for K and obtain:

2d + 2c = d + f/3 + 2g/3.

Solving the above for f:

f = 3d + 6c –2g. Arbitrary values can then be set for c and d, for which several values of g exist that will not render 3d + 6c – 2g a negative value. Based on these, a, b, e and h can also be obtained.





---

Solution to March 2002 Question of the Month

The question was:

What are we?

1. Our occurrence, I, approximately decreases by a factor of 50 for each 10-fold increase in energy, E.
   I₂=I₁/50^log(E2/E1).
2. We come from exotic places and have been trapped, accelerated and redirected by the galaxy's magnetic field.
3. Our low-energy variety leads to the formation of carbon-14 and beryllium-10. Our collisions also cause about 5 muons to pass through your head every second.
4. We influence the rate of mutation and therefore play a key role in the evolution of species.

Solution:

Cosmic rays are actually particles--mostly protons---that move almost at the speed of light and collide with molecules in our upper atmosphere. They were named by Robert Millikan, but discovered in about 1912 by the 1936 Physics Nobel Prize winner Victor Hess, who equipped high-flying balloons with electrometers. An electrometer is an instrument that measures the voltage between two electrostatically- charged bodies. Hess could not get rid of the background reading of his instrument, and, to his astonishment, he found that the reading kept increasing with altitude. The co-winner of the 1936 prize was Anderson, who discovered positrons (the positively charged electrons of anti matter) while investigating the nature of cosmic rays.

Read more about cosmic rays.

---

Solution to April 2002 Question of the Month

The question was:

One of the characteristic smells of barbecue smoke is caused by acrolein, an eye-irritant with the formula C₃H₄O. It is formed when heat breaks down glycerol, itself a breakdown product of fat. The formula of glycerol is C₃H₈O₃. From the formulas alone, how can you tell that glycerol does not gain or lose electrons in forming acrolein?

Solution:

Since glycerol is C₃H₈O₃, 3x + 8(+1) +3(-2) = 0, where x= C's oxidation number. x turns out to be -2/3. But for acrolein(C₃H₄O), 3x +4(1) +(-2) = 0, x is again -2/3. The oxidation number of carbon remains constant, so this indicates that the electrons of glycerol are just reshuffled internally under the stress of heat, the molecule decomposes, and two water molecules are expelled as glycerol turns to acrolein.

In industry, the "BBQ method" is essentially how acrolein is made. Glycerol vapour is decomposed at 330 to 340 ^oC, but the difference lies in the fact the vapour is passed over MgSO₄. Acrolein is an aldehyde with the following structural formula.
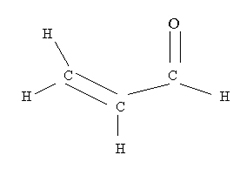Barbecues also create another aldehyde, formaldehyde, the same substance that is used to preserve specimens in biology labs. Formaldehyde kills bacteria which explains why meats cured with smoke don't spoil.

What happens in the mouths of carnivores when the meat is devoured? Yes it is chewed, but are there any other chemicals in the cooked meat that make it appealing? The meaty flavour seems to be a combination of IMP ( inosine monophosphate, a breakdown product of ATP, the "energy-giving molecule" which facilitates a host of reactions in living cells) and MSG, monosodium glumate, the salt version of glutamic acid, the same substance that is used as a food additive, especially in American Chinese restaurants. Mushrooms also contain a variety of glutamic acids. For this reason, certain mushrooms (example Portobellos)that have the right combination of texture and such chemicals are very meat-like in taste.


References


Atkins, P.W. Molecules Scientific American Library 1987

Merck Index Thirteenth Edition 1996

---

Solution to May 2002 Question of the Month

The question was:

• A hot plate's heating area is 210 cm².
• On the plate there is a flask containing 200 g of a liquid.
• The area of the flask that is actually in contact with the heat is 30 cm².
• The power rating of the hot plate is 600 W.
• It takes 495 seconds for the liquid to go from 20^oC to 70^oC.
What is the liquid's specific heat?

Solution:

The total energy emitted by the hot plate is E = Pt = 600 (J/s)(495 s)= 29700 J.
But out of this 29700 J, only 30/210 is absorbed because that's the fraction of the area in contact with the hot plate(the rest escapes), so Q = 29700(30/210)J = 4243 J
Q = mc DT
4243 J = 200c(70-20)
c = 4.25 J/(g C)
,probably water(experimental error accounts for small difference)

---

Solution to June 2002 Question of the Month

The question was:

Dinosaurs became extinct 65 million years ago. The present universe's entire history (assume 15 billion years) can be condensed to 1 calendar year (non-leap year). On this calendar, on what date and at what hour did dinosaurs become extinct?

Solution:

On this calendar, dinosaurs became extinct 65 X 10⁶y/(15 X 10⁹y)*365 days = 1.5817 days from the tail end on Dec 31 24:00 h. 1 day ago would be Dec 31 at 12 am. 2 days ago would would be Dec 30: 12 am. To get the time, we have to move forward from Dec 30 12 am, so the time is (2-1.5817)*24h = 10 am. This of course is assuming that we are certain of the 15 billion figure. Otherwise, the date itself is an approximation, and the time itself, meaningless. But it does show how recent the extinction is from the universe's point of view.

---

2nd June Puzzle:

The question was:

This one is from an old Quirks and Quarks episode in which Crawford of McGill asks, "You have two apparently identical iron bars but only one is a bar magnet; the other is unmagnetized iron. With no other equipment, what simple experiment will help you tell them apart?"

2nd June Puzzle Solution:

Make a T-formation with the two magnets. If they stick together then the the vertical bar is the bar magnet. If they do not attract, then the horizontal bar is the magnet because its center will have magnetic field lines that run parallel to the edge of the vertical bar and so will not attract it.

---

Solution to July 2002 Question of the Month

The question was:

We recently had people over for dinner, and, although I was a good host for most of the evening, when the conversation shifted towards the topic of cars, I tried to calculate how much warmer a room gets from absorbing body heat. Try to list all the relevant factors, formulas and physical constants needed for such an estimate.

Solution:

Assuming that there is no air conditioning, no open windows, and very good insulation, you would have to know:

1. the number of people in the room.
2. what activity (talking, dancing, thinking science) most are engaged in
3. the average number of food calories consumed by such activities.
4. the conversion factor used to turn food Calories into joules (X 4190)
5. the specific heat of air in J/(g C)
6. the dimensions of the adjacent rooms in meters (to be converted to volume in m³, and the density of air in g/m³ so that the mass of air can be calculated using mass = density X volume
7. In spite of good insulation, how much heat still escapes to the rest of the house and to the exterior, which depends on the difference in temperature between different rooms and on the external temperature.
8. The formula Q = mcDT, where Q = total heat generated; m = mass of air calculated in step (8) ; c = specific heat mentioned in step (7); and DT is the temperature change we are seeking.

So let's try it: assume 16 people just eating and talking for 4 hours. Each person consumes an average of 71 Calories doing so. Air has a specific heat of 1.0 J/(g/C) and a density of 0.00129 g/cm³ = 1290 g/m³. The adjacent rooms have a volume of 3 m X 10 m X 6 m, and an area of 60m²

The dining area loses 69000 J/(h m²)

Q = mcDT

71 Cal/(person*h)*4190 J/Cal * 16 people*4h - 69000J/(h m²)*(4 h)*(60m²)= 180 m³(1290 g/m³)(1.0 J/(g/C))DT

DT = 10 C: very roughly. So it's not the dull conversation that makes you sweat around the collar; it's body heat concentrated in a small space.

---

Solution to August 2002 Question of the Month

The question was: Of all naturally occurring elements possessing an even number of protons, how many have, as their most common stable isotope, a nucleus with an odd number of neutrons?

Solution:

Only 1. Beryllium. Be-9 is unique. All other natural elements with even atomic numbers have an even number of neutrons as their most common isotope.

In the atomic nucleus there are transition states for protons and neutrons, just like there are for electrons. Nucleons (protons or neutrons) can move from a ground state to an excited state. For nuclei with an even number of both protons and neutrons, there is only one excited state for these particles, and the gap between the two states is relatively large.


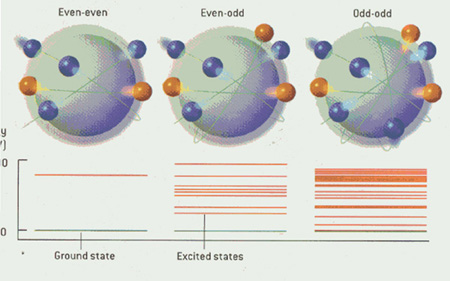
This occurs because each proton pairs off with a neutron. If the mass number is even, there is no "leftover" nucleon. When there is an extra neutron, there are many "in between" transition states created for that particle. This explanation, however, cannot account for the stability of isotopes with an odd number of protons ( like ₁₅P-31, ₁₁Na-23, ₁₉K-39) which also have an unpaired neutron.

Be-9 was probably synthesized during the Big Bang but in very small amounts. Why it's more stable then Be-8 is another mystery.

Part 2 Solution

The question was

After several students spelled "noble" n-o-b-e-l on a review test, I wondered if any discoverers of noble gases were ever awarded a Nobel prize. Has such a thing ever happened?

Solution:

William Ramsay received the 1904 Nobel Prize in chemistry for discovering Ne,Ar,Kr and Xe. Taking a hint from an experiment by Cavendish in which he had measured a small amount of gas leftover from a reaction between nitrogen and oxygen, Ramsay finally explained why the density of nitrogen samples obtained from air was higher than the density of nitrogen extracted from ammonia. They contained small amounts of unknown gases that behaved like helium.

---

Solution to September 2002 Question of the Month

The question was:

This, as they say in the movies, is based on a true story. Even with sophisticated medical technology at their fingertips, doctors can still rely on simple observations. For example,with experience and a stethoscope, they can tell a great deal about our heart and lungs. They can also look into our ears and eyes, both of which can tell a medical story. But to base a diagnosis only on the white of someone's eyes is a little extreme. There are such characters around, and one of them was visited by an old lady I know.

From peering into her gullible but otherwise good-looking eyes, he claimed to have seen a kidney condition. "Your kidneys are not too healthy", he asserted. Then he went on to prescribe some obscure oriental tea, which had to be drunk only after letting most of the water evaporate from the extract.

The woman went out and bought the product, prepared it as suggested by the character and drank it.

Two days later, after a few hours of excruciating back pains and other severe discomfort in her urinary tract, upon peeing she noticed a sandy residue at the bottom of the toilet bowl. The pain persisted for a few more hours, but she was fine the next morning.

The woman was convinced that the "prescription" had cleansed out her excretory system.

Is there another possible explanation for what she experienced?

Solution: There is a possibility that his prescription actually caused the adverse reaction. Tea, in general, is rich in oxalates, and his recommended tea may have had an unusually high amount of the ion. Recall that the tea solution was also concentrated since water was purposely evaporated. This may have been enough to form small crystals of calcium oxalate or kidney stones within her system. What the woman experienced was definitely symptomatic of passing stones, but whether a single dose of the tea could have induced such a condition is speculation on my part.

---

Solution to October 2002 Question of the Month

The question was:

If a planet with half of the Earth's density weighed 32 times as much as the Earth, how much longer would it take to go around that planet?




Solution:

If the planet was only half as dense then it must have had 2 X 32 = 64 times the volume. Think about it: mass / volume = density. But for the planet to be 64 times as voluminous as the earth, it only has 4 times the radius( volume is the result of the radius cubed, and the cube root of 64 is 4.) If it is four times as wide it will, have four times the circumference (since circumference is pX diameter), and it will take four times longer to go around that planet, assuming the same speed of course.

---

Solution to November 2002 Question of the Month

The question was:

A white dwarf is a dense stellar object.( How dense? 10⁵ to 10⁸ g/cm³, so it roughly has the mass of the sun crammed into something the size of the earth.) While a star shines, the pressure from its internal radiation is balanced by gravity, so our sun, for example,remains more or less the same size. But when a star "dies out" (stops fusing nuclei), it risks collapsing under its own gravity. A white dwarf, however, is supported against collapse under self-gravity by the degeneracy pressure of electrons.(The Pauli exclusion principle states that no two electrons can occupy the same quantum state.)

White dwarfs, which consist mainly of carbon and oxygen ( see evolution of the elements), are formed as the evolutionary end products of stars of relatively low mass (about that of the sun); high-mass stars may end up as neutron stars or black holes.


Enough already! Let's get to the question. What would happen if a white dwarf somehow collided with our sun?

Solution: According to Michael Shara's article in the November, 2002 issue of Scientific American, a main sequence star such as our sun would be highly compressed and the ensuing pressure would cause the sun to blow itself apart in a matter of a few hours. Meanwhile,the denser white dwarf (10 million times denser) would pass through the sun relatively unscathed. Its outer layers would be warmed; there would be more nitrogen on its surface, but other than that, there would be no other sign of a collision. Luckily for our sun, such an encounter is highly unlikely.

---

Solution to December 2002 Question of the Month

The question was:

Consider two pieces of zinc of negligible thickness sitting at the bottom of a beaker. The first piece of zinc is shaped like a flat disk with a hole in the middle. Its dimensions are revealed in the diagram below (see piece A). Ring B is smaller in diameter but thicker, as shown. 6 M HCl is added to the beaker.

Which piece of zinc will disappear faster? Why?.

They should react at exactly the same rate. Since thickness is negligible and all other factors are equal, the rate of reaction will depend only on area. But their areas are equal. Not convinced?

Page Maintained by E. Uva; euva@retired.ca

Copyright ©2002

Created:April/6/1996; Updated: Apr/29/2003